Объяснение:
![\[\begin{gathered}{x^2}-6x-160\hfill\\{x^2}-6x-16=0\hfill\\D={b^2}-4ac=36+64=100\hfill\\{x_{1,2}}=\frac{{-b \pm \sqrt D}}{{2a}}=\frac{{6\pm \sqrt{100}}}{{2\cdot1}}=\frac{{6\pm 10}}{2}\hfill\\{x_1}=\frac{{6+10}}{2}=\frac{{16}}{2}=8\hfill\\{x_2}=\frac{{6-10}}{2}=\frac{{-4}}{2}=-2\hfill\\\end{gathered}\]](/tpl/images/1017/1636/274ee.png)
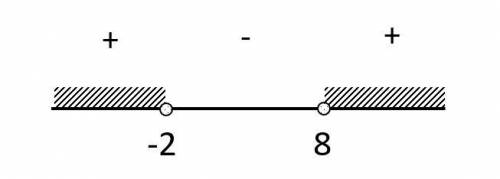
Отметим корни на числовой прямой и выясним знаки на полученных интервалах.
![\[\boxed{x\in(-\infty;-2)\cup(8;+\infty)}\]](/tpl/images/1017/1636/83bc4.png)
Пусть боковая сторона равнобедренного треугольника - х см, тогда основание треугольника будет 18-2х или 2(9-х) см.
Составим выражение для высоты треугольника, проведенной к основанию
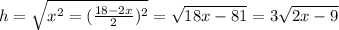
Теперь составим выражение площади треугольника

Найдем производную полученного выражения

при x<6 значение производной S'>0, а при x>6 S'<0, значит при х=6 функция S принимает максимальное значение (максимум функции)
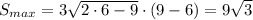
Таким образом, плащадь треугольника будет наибольшей, если все его стороны будут равны 6 см, т.е. он будет равносторонним.

D= B² -4ac= 36 + 64 = 100 = 10
x1,2 = -b ± ✓d 6±10
=
2a 2
x1 = 8
x2 = -2