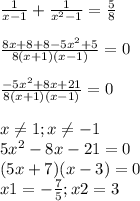1) Cosx = t
6t² + t -1 = 0
D = b² -4ac = 1 - 4*6*(-1) = 25 > 0
t₁ = (-1+5)/12 = 4/12 = 1/3
t₂ = (-1 -5)/12 = -1/2
a) Cosx = 1/3 б) Сosx = -1/2
x = +-arcCos(1/3) + 2πk , k ∈Z x = +-arcCos(-1/2) + 2πn , n ∈Z
x = +- 2π/3 +2πn , n ∈ Z
2) учтём, что Cosx = 2Cos²x/2 -1
наше уравнение:
Cosx/2 = 1 + 2Cos²x/2 -1
Cosx/2 = t
2Cos²x/2 - Cosx/2 = 0
Cosx/2(2Cosx/2 -1) = 0
Cosx/2 = 0 или 2Cosx/2 -1 = 0
x/2 = π/2 + 2πk , k ∈Z Cosx/2 = 1/2
x = π + 4πk , k ∈ Z x/2 = +-arcCos(1/2) + 2πn , n ∈ Z
x/2= +- π/3+ 2πn , n ∈ Z
x = +-2π/3 + 4 πn , n ∈ Z
1) Cosx = t
6t² + t -1 = 0
D = b² -4ac = 1 - 4*6*(-1) = 25 > 0
t₁ = (-1+5)/12 = 4/12 = 1/3
t₂ = (-1 -5)/12 = -1/2
a) Cosx = 1/3 б) Сosx = -1/2
x = +-arcCos(1/3) + 2πk , k ∈Z x = +-arcCos(-1/2) + 2πn , n ∈Z
x = +- 2π/3 +2πn , n ∈ Z
2) учтём, что Cosx = 2Cos²x/2 -1
наше уравнение:
Cosx/2 = 1 + 2Cos²x/2 -1
Cosx/2 = t
2Cos²x/2 - Cosx/2 = 0
Cosx/2(2Cosx/2 -1) = 0
Cosx/2 = 0 или 2Cosx/2 -1 = 0
x/2 = π/2 + 2πk , k ∈Z Cosx/2 = 1/2
x = π + 4πk , k ∈ Z x/2 = +-arcCos(1/2) + 2πn , n ∈ Z
x/2= +- π/3+ 2πn , n ∈ Z
x = +-2π/3 + 4 πn , n ∈ Z
1) y1=-6; y2=5
2) x1=7/5; x2=3
Объяснение:
1)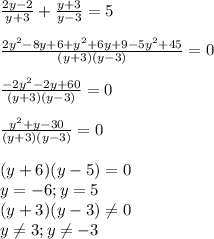
2)