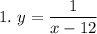
Ограничение только на неравенство нулю знаменателя:

![\displaystyle 2. \ y=\sqrt[12]{5-x}](/tpl/images/1018/8370/70d19.png)
У нас корень четной степени, а значит, ограничением является неотрицательность подкоренного выражения:
![5-x \geq 0 \Rightarrow x \leq 5 \Rightarrow \boxed{x\in(-\infty; 5]}](/tpl/images/1018/8370/7f5b5.png)
По поводу 3-его у меня сомнения в правильности записи условия:
если условие такое, как записано, то есть
![y= \dfrac{1}{\sqrt[4]{x^2}-11x+10}](/tpl/images/1018/8370/c6591.png) , то ограничение лишь на неравенство нулю знаменателя:
, то ограничение лишь на неравенство нулю знаменателя:
![\sqrt[4]{x^2}-11x+10 \neq 0; \sqrt[n]{x^2}=\sqrt[\frac{n}{2}]{|x|}](/tpl/images/1018/8370/c6fa2.png)
В данном случае получаем:
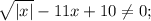
Рассматриваем 2 случая:
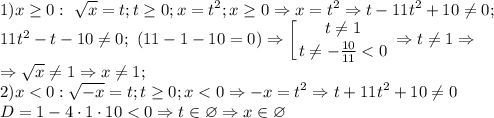
То есть 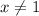
Но я сильно сомневаюсь, что там не все под корнем, рассмотрим этот случай:
![\displaystyle y=\frac{1}{\sqrt[4]{x^2-11x+10} } \Rightarrow \left \{ {{x^2-11x+10 \geq 0} \atop {x^2-11x+10\neq 0}} \right. \Rightarrow x^2-11x+100; \\ x^2-10x-x+100; x(x-10)-(x-10)0; (x-10)(x-1)0](/tpl/images/1018/8370/c2fb5.png)
Чтобы решить неравенство 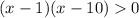 воспользуемся методом интервалов, нули уже нашли
воспользуемся методом интервалов, нули уже нашли 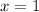 и
и 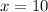 , имеем +-+ на промежутках и
, имеем +-+ на промежутках и 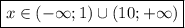
Пусть первоначально с первого участка было собрано х тонн, а со второго у тонн клевера. По условию задачи всего в первый год было собрано 460 тонн.
Составляем уравнение:
х+у=460
Во второй год с первого участка было собрано на 15% больше клевера, т.е. 1,15х, а со второго на 10% клевера больше, т.е. 1,1у.
По условию во второй год всего собрали 516 тонн клевера.
Составляем уравнение:
1,15х+1,1у=516
Решаем систему уравнений:
х+у=460
1,15х+1,1у=516
х=460-у
1,15(460-у)+1,1у=516
529-1,15у+1,1у=516
-0,05у=516-529
-0,05у=-13
у=-13:(-0,05)
у=260(тонн)-собрали со второго участка в первый год
х=460-260=200(тонн)-собрали с первого участка в первый год
Пусть первоначально с первого участка было собрано х тонн, а со второго у тонн клевера. По условию задачи всего в первый год было собрано 460 тонн.
Составляем уравнение:
х+у=460
Во второй год с первого участка было собрано на 15% больше клевера, т.е. 1,15х, а со второго на 10% клевера больше, т.е. 1,1у.
По условию во второй год всего собрали 516 тонн клевера.
Составляем уравнение:
1,15х+1,1у=516
Решаем систему уравнений:
х+у=460
1,15х+1,1у=516
х=460-у
1,15(460-у)+1,1у=516
529-1,15у+1,1у=516
-0,05у=516-529
-0,05у=-13
у=-13:(-0,05)
у=260(тонн)-собрали со второго участка в первый год
х=460-260=200(тонн)-собрали с первого участка в первый год
Решение приложено...