-32zx + 40zy - 56z = -4z ( 8x - 10y + 14 )
Объяснение:
Сперва надо найти общий множитель коэффициентов, то-есть поделить их на тот множитель, который делит все числа, выкинуть его за скобки, после надо найти общую букву (в данном случае z) потому что она стоит во многих числах этого примера, его тоже выносим за скобки и в скобках уже пишем числа, поделенные на -4, так как в 32zx, мы пишем только x, потому, что z уже есть в -4z и дальше ставим не плюс, а минус, потому что число, выведенное за скобки - отрицательное, делим 40 на 4 и получаем 10y, уже знаем почему и пишем + тоже зная почему, делим 56 на 4 и получаем 14 уже без числа, потому что у 56z есть z, а буква стоит в -4z. Вот мы и получили решение.
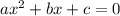) - некое число, необходимое для вычисления корней этого уравнения по формуле: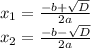
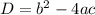
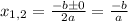), и не имеет если дискриминант меньше нуля(т.к. выражение стоящее под корнем(в нашем случает D) должно быть неотрицательно, то есть D≥0 ).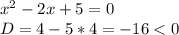
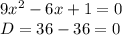
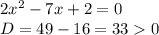
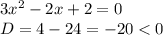
1. 1 ОДЗ х∈(-∞;+∞), т.к. дан многочлен.
2. с осью ох. у=0, х³-3х²+4=0, х=2, делим х³-3х²+4 на х-2, получаем
(х²-х-2)=(х+1)(х-2), чтобы разложить на множители, предварительно по теореме, обратной теореме Виета, угадали корни, это -1 и 2, итак, точек пересечения с осью ох найдено две (-1;0);(2;0). с осью оу х=0, тогда у=4, точка (0;4)
3. вертикальных нет, наклонные проверим к= предел при х, стремящемся к ∞ f(x)/x равен бесконечности, поэтому нет и наклонных асимптот.
4. y(-x)=-x³-3x²+4 ≠y(x) не является четной, y(-x)≠ -y(x) не является нечетной. это функция общего вида.
5.находим производную и точки экстремума и интервалы монотонности. у'=3х²-6х=0 зх*(х-2)=0; х=0;х=2, исследуя знак производной, получаем, что функция убывает на промежутке [0; 2] и возрастает на каждом из промежутков (-∞;0] и [2;+∞)
___02
+ - + точка х=0- точка максимума, х=2- точка минимума
6.находим вторую производную. 6х-6=0, точка х=1 точка перегиба, т.к. при переходе через нее вторая производная меняет знак с минуса на плюс. 1
- +
На промежутке (-∞;1) график функции выпуклый вверх, а на промежутке (1;+∞) вниз.
2z(-16x+20y-28)
Объяснение:Удачи)