1-ый случай, когда a>0, b>0, тогда точка A лежит в 1-ой координатной четверти. Следовательно, точка B лежит в 3-ей координатной четверти и не принадлежит графику функции y=x^2, так как это парабола, и обе ее ветви лежат в 1-ой и 2-ой к.четвертях. 2-ой случай, когда a>0, b<0, тогда точка A лежит в 4-ой координатной четверти. Этого не может быть, так как ветви параболы по условию находятся в 1 и 2-ой к.ч. 3-ий случай, когда a<0, b>0, тогда точка A лежит в 2-ой координатной четверти. Следовательно, точка B лежит в 4-ой координатной четверти и не принадлежит графику функции y=x^2. 4-ый случай, когда a<0, b<0, тогда точка A лежит в 3-ей к.ч. Этого не может быть, так как ветви параболы по условию находятся в 1 и 2-ой к.ч.
Если тебя не просят рассматривать случаи с различными знаками a и b, то доказательство идет другое. Координаты точки A имеют положительные знаки, отсюда следует, что она находится в первой координатной четверти. Координаты точки B имеют отрицательные знаки, отсюда следует, что она лежит в 3-ей координатной четверти, а значит, она не может принадлежать графику функции. Это будет отчетливо видно, если ты посмотришь на график этой функции.
-
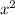+ 8х + 3х - 24 = -х (х - 3) + 8 (х - 3) = (х - 3) (8 - х)
-
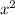- 11х + 2х + 22 = -х (х + 11) + 2 (х + 11) = (х + 11) (2 - х)
-
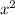- 17х + 3х + 51 = -х (х + 17) + 3 (х + 17) = (х + 17) (3 - х)
-2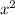
- 22х + 11х + 121 = -2х (х + 11) + 11 (х + 11) = (х + 11) (11 - 2х)
-4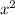
+ 10х - 12х +30 = -4х (х + 3) + 10 (х + 3) = (х + 3) (10 - 4х)
-5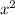
- 10х + 4х + 8 = -5х (х + 2) + 4 (х + 2) = (х + 2) (4 - 5х)
4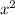
+ 16х - 5х - 20 = 4х (х + 4) - 5 (х + 4) = (х + 4) (4х - 5)
9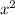
- 27х + 6х + 18 = 9х (х - 3) + 6 (х + 3)
В последнем, скорее всего, какая-то ошибка, потому что преобразовать его в произведение невозможно.