Мыслим логически: считаем куски сыра начиная от одного : 1,3,4,5,7,9.
Почему так?
1-условие не ограничивает
2=2*1-ограничено условием
3-условие не ограничивает
4-условие не ограничивает т.к. нет 2
5 -условие не ограничивает
6-ограничено условием, т.к. 6=2*3
7-условие не ограничивает
8-ограничено условием, т.к. 8=3*4
9-условие не ограничивает
10-ограничено условием, т.к. 10=2*5
Логика в том, что мы можем использовать все нечетные числа от 1 до 10 т.е. те которые не делятся на 2 без остатка: 1 3 5 7 9. А также числа,результат деления на 2 которых не дублирует ни одно из чисел предыдущего ряда(таким является число 4 для данной ситуации).
Также можно заменять любое нечетное k+1 число предыдущей последовательности на число (k+1)*2, если таковое не нарушает условия задачи. Например последовательность
1 3 5 7 9 4 можно заменить последвательностью 1 5 6 7 9 4, поскольку число 6 можно получить лишь делением 12 на 2, а т.к. 12 в данном ряде отсутствует мы можем записать в него число 6.
Вне зависимости от перестановок, максимальное числом мышей, сташивших сыр в задаче не может превышать 6.
ответ:6 мышей
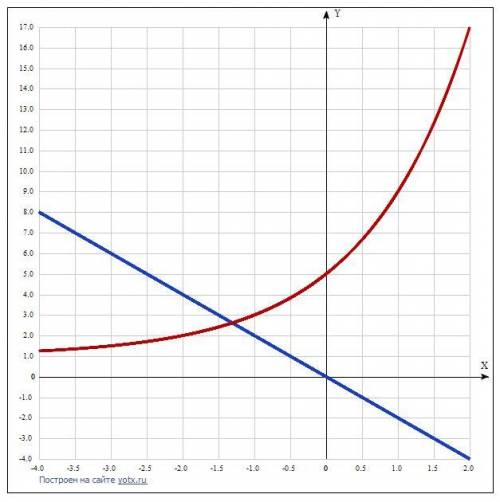
Для графического решения заданное уравнение представим как равенство двух функций: 2^(x + 2) + 1 = -2х.
Точка пересечения их графиков даст корень.
Прямая у = -2х строится по двум точкам, например, х = 0, у = 0.
х = -3, у = 6.
Для построения функции у = (2^(x+2)) + 1 приводит таблицу точек.
x y
-4.0 1.25
-3.5 1.35
-3.0 1.5
-2.5 1.71
-2.0 2
-1.5 2.41
-1.0 3
-0.5 3.83
0 5
0.5 6.66
1.0 9
1.5 12.31
2.0 17.
Точка пересечения х = -1,30785.
Сумма двух последовательных целых чисел, между которыми находится корень уравнения, равна (-2) + (-1) = -3.
Мыши могли украсть 10, 9, 8, 7, 6, 2 куска сыра. Соответственно, никто из мышей не украл 5, 4, 3 или 1 кусок сыра, так как 10=5*2; 8=4*2; 6=3*2; 2=1*2. Получается, что мышек-воришек было не больше 6.
ответ: 6.