![\displaystyle \tt d). \ (\sqrt[3]{7}+3)(\sqrt[3]{49}-3\sqrt[3]{7}+9) \ \ \ \ \ | \ \sqrt[3]{7}=a\\\\{} \ \ \ \ (a+3)(a^{2}-3a+3^{2})=a^{3}+3^{3}=(\sqrt[3]{7})^{3}+27=7+27=34;\\\\\\b). \ \frac{61}{16+4\sqrt[3]{3}+\sqrt[3]{9}}+\sqrt[3]{3}=\frac{61(4-\sqrt[3]{3}) }{(4-\sqrt[3]{3})(4^{2}+4\sqrt[3]{3}+(\sqrt[3]{3})^{2})}+\sqrt[3]{3}=\\\\\\{} \ =\frac{61(4-\sqrt[3]{3})+\sqrt[3]{3}(4^{3}-(\sqrt[3]{3})^{3})}{4^{3}-(\sqrt[3]{3})^{3}}=\frac{244-61\sqrt[3]{3}+61\sqrt[3]{3} }{64-3}=4;](/tpl/images/1020/4656/98bfe.png)

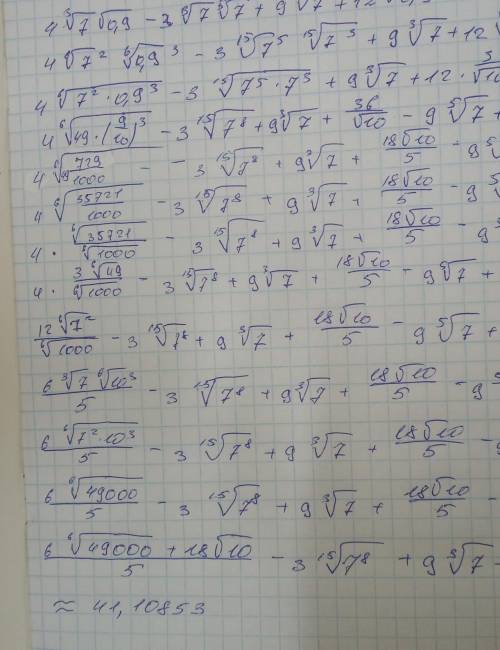
решение к первому примеру
1.Область определения функции явяется луч [0;+∞);
2. y=0 при х=0 из этого следует что начало координат принадлежит графику функции; y>0 при x>0, а значит график располагается в первой координатной четверти (первом координатном угле)
3. Функция возрастает на луче [0;+∞); Другими словами на этом луче, большему значению аргумента, соответствует большее значение функции.
4. Функция имеет наименьшее значение, и не имеет наибольшего значения. Данное значение достигается тогда, когда х=0;
5. Функция непрерывна.
6. Функция выпукла вверх.
7. Область значений функции y=√x является луч [0;+∞)
Следует отметить, что график функции y=√x симметричен относительно оси симметрии у=х с графиком функции y=x^2, при x>0.
Полиглоты-люди,знающие множество языков.Согласитесь,такие люди много где нужны,да и профессию им найти несложно, причем хорошую. Такие люди обладают огромной силой воли и терпением, потому-что выучить незнакомый язык,да ещё и не один,не так уж легко.Также таким людям не составит труда поехать жить в другую страну,ведь им не придется везде ходить со словарем.
Они легко смогут найти друзей по интересам в разных частях света,и вообще,есть куча интересных занятий и большой выбор профессии
Объяснение: