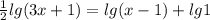
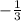, x > 1 ⇒ x > 1. 
при условии существования логарифмов. В нашем случае это тоже работает: данные логарифмы десятичные, значит, в основании 10. Вспомним, что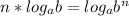 
(также при условии существования логарифма). Сразу вычислим lg1 - чтобы получить из 10 1, нужно 10 возвести в нулевую степень, значит, что 0. Тогда наше уравнение равносильно такому: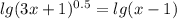 
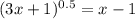
task/29523226 Найдите тангенс угла наклона касательной к графику функции y=x²-5x+4 в точке ( допустим ) x₀ =3 .
Геометрический смысл производной заключается в том, что численно производная функции в данной точке равна тангенсу угла, образованного касательной, проведенной через эту точку к данной кривой, и положительным направлением оси Ох.
tgα = f '(x₀) , где α → угол наклона ...
f '(x) = y '= (x²- 5x+4 ) ' = 2x - 5⇒ f '(x₀) =2x₀ - 5 ; tgα =2x₀-5 =2*3 -5 = 1 .
* * * угол с осью абсцисс 45° * * *