Question

2.75. 1) найдите коэффициенты риq, если — корни уравнения
х4 + px + q = 0, а суммы и+ 1 и + 1- корни уравнения х2 - p=х+ pq = 0.
2) и и v — корни уравнения х? – 8х + 12 = 0. напишите квадратное
1 1
уравнение, если его корни равны а и​

Answer 1

1) p=1, q-любое; p=-2, q=-1.

2) 1728x²-224x+1=0

Объяснение:

2.75.1)

Если u, v - корни уравнения x²+px+q=0, то u+v=-p, uv=q.

Если u+1, v+1 - корни уравнения x²-p²x+pq=0, то (u+1)+(v+1)=p², (u+1)(v+1)=pq.

Получились уравнения:

u+v=-p,

uv=q,

(u+1)+(v+1)=p²,

(u+1)(v+1)=pq.

Выпишем третье уравнение: (u+v)+2=p². Подставим туда первое уравнение: -p+2=p². Отсюда p²+p-2=0, откуда p=1 или p=-2.

Рассмотрим 4 уравнение: uv+(u+v)+1=pq. Подставим туда 1 и 2 уравнения: q-p+1=pq, откуда (p-1)(q+1)=0. То есть p=1 или q=-1.

Получим систему из совокупностей уравнений.

$\left \{ {{\left[\begin{gathered}p=1; \\p=-2, \\ \end{gathered} \right.} \atop {\left[\begin{gathered}p=1; \\ q=-1, \\ \end{gathered} \right.}} \right.$

Если p=1, то q - любое значение

Если q=-1, то p=1 или p=-2

Окончательный ответ: p=1, q-любое; p=-2, q=-1.

2.75.2)

$x^2-8x+12=0\\D=(-8)^2-4*12=16\\x_1=\frac{8-\sqrt{16}}{2}=2\\x_2=\frac{8+\sqrt{16}}{2}=6$

Новые корни уравнения: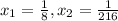 $x_1=\frac{1}{8},x_2=\frac{1}{216}$

Искомое квадратное уравнение:

$x^2-(\frac{1}{8}+\frac{1}{216})x+\frac{1}{8*216}=0\\1728x^2-(216+8)x+1=0\\1728x^2-224x+1=0$