Нет, не могли. Среди чисел от 1 до 72 имеется ровно 72/9=8 чисел кратных 9. Среди чисел от 1 до 72 имеется ровно 72/3-72/9=16 кратных 3, но не кратных 9. Найдем максимально возможное количество столбцов, в которых произведения их элементов будут кратны 9. Максимальное количество таких столбцов может получиться, когда все числа кратные 9 находятся в разных столбцах, а числа кратные только 3 (но не кратные 9) находятся по два в каждом столбце. Итак, максимальное количество столбцов, в которых произведения четверок кратны 9 равно 16/2+8=16. По признаку делимости на 9 сумма цифр произведений элементов таких столбцов тоже кратна 9. Значит среди полученных сумм цифр не более 16 штук кратны 9, и кратные 9 среди них обязательно будут. Значит суммы цифр для всех столбцов не могут быть равными, т.к. иначе суммы цифр всех 18 произведений были бы кратны 9, а мы только что вывели, что их не более 16 штук. Противоречие.
Нет, не могли. Среди чисел от 1 до 72 имеется ровно 72/9=8 чисел кратных 9. Среди чисел от 1 до 72 имеется ровно 72/3-72/9=16 кратных 3, но не кратных 9. Найдем максимально возможное количество столбцов, в которых произведения их элементов будут кратны 9. Максимальное количество таких столбцов может получиться, когда все числа кратные 9 находятся в разных столбцах, а числа кратные только 3 (но не кратные 9) находятся по два в каждом столбце. Итак, максимальное количество столбцов, в которых произведения четверок кратны 9 равно 16/2+8=16. По признаку делимости на 9 сумма цифр произведений элементов таких столбцов тоже кратна 9. Значит среди полученных сумм цифр не более 16 штук кратны 9, и кратные 9 среди них обязательно будут. Значит суммы цифр для всех столбцов не могут быть равными, т.к. иначе суммы цифр всех 18 произведений были бы кратны 9, а мы только что вывели, что их не более 16 штук. Противоречие.
при a=8
Объяснение:
1. Рассмотрим, когда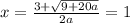
Значит, при a=8
2. Рассмотрим, когда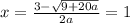
Решений нет (т.к. если подставлять эти корни)