Объяснение:
1) F(x)=(x^4)/4-3x³/³+5x²/2-x +C, где С- некоторая постоянная
F(x)=(x^4)/4-x³+2,5x²-x +C, где С- некоторая постоянная
2)f(x)=sin(2x+5)
F(x)=-0,5×cos(2x+5)+C, где С- некоторая постоянная
3)f(x)= √x+7
F(x)=2/3×(x+7)^1,5+C, где С- некоторая постоянная
f(x)=3(x^2-2x)=3х²-6х
F(x)=3х³/3-6х²/2 +C, где С- некоторая постоянная
F(x)=х³-3х²+C, где С- некоторая постоянная
F(x)=x^3-3x^2+5 - является одной из первообразных для f(x)=3(x^2-2x)
4 (м) ткани на 1 платье.
2 (м) ткани на 1 юбку.
Объяснение:
На изготовление четырех платьев и пяти юбок израсходовали двадцать шесть метров ткани, а на изготовление шести платьев и четырех юбок израсходовали тридцать два метра ткани. Сколько ткани потребуется на пошив одного платья и сколько ткани потребуется на пошив одной юбки?
х - ткани на 1 платье
у - ткани на 1 юбку
Согласно условию задачи составляем систему уравнений:
4х+5у=26
6х+4у=32
Разделим второе уравнение на 4 для упрощения:
4х+5у=26
1,5х+у=8
Выразим у через х во втором уравнении, подставим выражение в первое уравнение и вычислим х:
у=8-1,5х
4х+5(8-1,5х)=26
4х+40-7,5х=26
-3,5х=26-40
-3,5х= -14
х= -14/-3,5
х=4 (м) ткани на 1 платье.
у=8-1,5х
у=8-1,5*4
у=8-6
у=2 (м) ткани на 1 юбку.
Проверка:
4*4+5*2=26
6*4+4*2=32, верно.
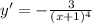
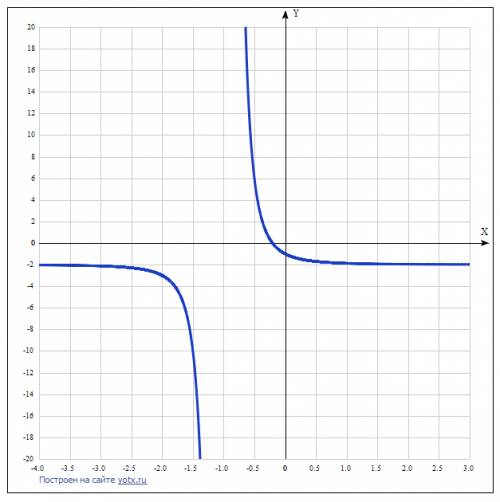
для функции f(x)
Объяснение: