Решите систему :
{ (1/3x +1/4y+5/12z)(x/3+y/4+5z/12) =1 ;
{ x³+3y²-7z =6
{xy > 0
{xz >0
{yz >0
ответ: (2 ; 2 ;2) ;
((-5-√13)/2;(-5-√13)/2;(-5-√13)/2 ) , ( (-5+√13)/2 ;(-5 +√13)/2 ;(-5+√13)/2).
Объяснение: Область Определения Системы x ≠0 ,y ≠0 , z ≠0
Очевидно( показывают три неравенство системы) , переменные системы x , y и z одного знака .
{ (1/3x +1/4y+5/12z)(x/3+y/4+5z/12) =1 ;
{ x³+3y²-7z =6
* * * (x/y+y/x -2) = (x²-2xy+y²) /xy = (x-y)²/xy ≥0 и т.д * * *
Удачи ! Решение во вложение
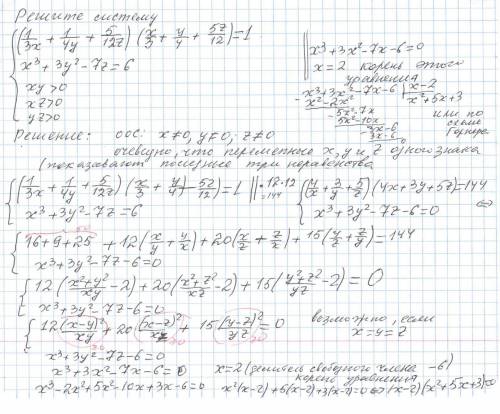
1. Найдите значение выражения:
а) 0,6(4×5 −14) −0,4(5×5−1)=12-8,4-10+0,4=-6
б) 1,2(1,2 −7) −1,8(3 −1,2)=1,44-8,4-5,4+2,16=-10,2
2. Приведите подобные слагаемые:
а) 8в + 12а −21в + а=-13b+13a
б) 9а + 17в−30а + 4в=-21a+21b
3. Раскройте скобки и приведите подобные слагаемые:
а) −(3с + 5х) −(9с −6х)=-3c-5x-9c+6x=-12c+x
б) (2а −7у) − (5а −7у)=2a-7y-5a+7y=-3a
4. Решите уравнение:
а) (6х + 1) −(3 −2х) = 14
6x+1-3+2x=14
8x-2=14
8x=14+2=16
x=16÷8=2
б) 9 −(8х −11) = 12
9-8x+11=12
20- 8x=12
-8x=12-20=-8
x=-8÷(-8)
x=1
5. Упростите выражение:
а) 19у + 2(3 −4у) + 11у=19y+6-8y+11y=22y+6
б) 33 −8(11в −1) −2в=33-88b+8-2b=41-90b