Объяснение:
1
\begin{gathered}1 - 8 \sin(2 \beta ) \times \cos( 2\beta ) = 1 - 4 \times 2 \sin( 2\beta ) \cos( 2\beta ) = \\ = 1 - 4 \sin( 4\beta ) \end{gathered}
1−8sin(2β)×cos(2β)=1−4×2sin(2β)cos(2β)=
=1−4sin(4β)
2
\begin{gathered}tg \beta (1 + \cos(2 \beta ) - \sin( 2\beta ) = \\ = tg \beta \times (1 + { \cos }^{2} (\beta) - { \sin}^{2}( \beta )) - \sin( 2\beta ) = \\ = tg \beta \times 2 { \cos }^{2} (\beta ) - \sin( 2\beta ) = \\ = 2 \sin( \beta ) \cos( \beta ) - 2 \sin( \beta ) \cos( \beta ) = 0\end{gathered}
tgβ(1+cos(2β)−sin(2β)=
=tgβ×(1+cos
2
(β)−sin
2
(β))−sin(2β)=
=tgβ×2cos
2
(β)−sin(2β)=
=2sin(β)cos(β)−2sin(β)cos(β)=0
3
\begin{gathered} \frac{2 \sin( \beta ) - \sin( 2\beta ) }{ 2\sin( \beta ) + \sin( 2\beta ) } = \\ = \frac{2 \sin( \beta ) - 2 \sin( \beta ) \cos( \beta ) }{ 2\sin( \beta ) + 2 \sin( \beta ) \cos( \beta ) } = \\ = \frac{2 \sin( \beta )(1 - \cos( \beta )) }{ 2\sin( \beta ) (1 + \cos( \beta )) } = \frac{1 - \cos( \beta ) }{1 + \cos( \beta ) } \end{gathered}
2sin(β)+sin(2β)
2sin(β)−sin(2β)
=
=
2sin(β)+2sin(β)cos(β)
2sin(β)−2sin(β)cos(β)
=
=
2sin(β)(1+cos(β))
2sin(β)(1−cos(β))
=
1+cos(β)
1−cos(β)
4
\begin{gathered} \frac{ctg(45 - \beta )}{1 - {ctg}^{2}(45 - \beta ) } = - \frac{ctg(45 - \beta )}{ {ctg}^{2} (45 - \beta ) - 1} = \\ = - \frac{2ctg(45 - \ \beta )}{2( {ctg}^{2}(45 - \beta ) - 1) } = - \frac{1}{2ctg(45 - \beta )} \end{gathered}
1−ctg
2
(45−β)
ctg(45−β)
=−
ctg
2
(45−β)−1
ctg(45−β)
=
=−
2(ctg
2
(45−β)−1)
2ctg(45− β)
=−
2ctg(45−β)
1
1) Область определения функции sinx, а также sin2x это множество R всех действительных чисел. Но в нашем случае sin2x стоит в знаменателе, а на 0 делить нельзя. Значит из множества R надо исключить все значения 2x при которых sin2x =0, а это значения аргумента 2x = 180n n - все целые числа положительные и отрицательные, включая 0. Таким образом, область определения функции это множество R за исключением значений x = 90n Примечание : значения x даны в градусах. Чтобы перевести в pi, помните, что pi=180° 2) Решение аналогично предыдущей задаче. Разница в том, что cosx принимает значение 0 при x = 90+180n, а cosx/2 принимает значения 0 при x=45+90n. Значит область определения функции это множество R за исключением значений x = 45+90n Извини, Дима, за предыдущие ответы. Торопился на совещание.
Умножим левую и правую части уравнения на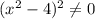
, получаем
В левой части уравнения применим формулу разность квадратов
Произведение равно нулю, если хотя бы один из множителей равен нулю
Корни x = ±2 посторонние, так как на 0 делить нельзя.
ответ: ± 3.