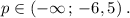5х²-10-2р-3=0
5х²-(2р+13)=0
D=0+4*5*(2p+13)<0 (4*5>0), значит
2p+13<0
p<-6,5
p∈(-∞; -6,5)
1) a^2b-2b+ab^2-2a=ab(a-b)-2(a-b)=(a-b)(ab-2)
2)x-y-3x^2+3y^2=(x-y)-3(x^2-y^2)=(x-y)-3(x-y)(x+y)=(x-y)(1-3x-3y)
3) a-3b+9b^2-a^2=(a-3b)+(3b-a)(3b+a)= -(a-3b)(1+3b+a)
4)x^2 y-x^2-xy+x^3=x^2(y+x)-x(x+y)=(x+y)(x^2-x)
5)a^2-9b^2+18bc-9c^2=a^2-(9b^2-18bc+9c^2)=a^2-(3b-3c)^2=(a-3b+3c)(a+3b-3c).
6)3a²+12b²+12ab-12=3(a²+4ab+4b²)-12=3(a+2b)²-12=3((a+2b)²-4)=3(a+2b-2) (a+2b+2)
7)x^3 y²-xy-x^3+x=xy(x-1)-x(x²-1)=xy(x-1)-x(x-1)(x+1)=(x-1)(xy-x²-x)
8)a² b-ab²-ac+ab+bc-c=ab(a-b+1)-c(a-b+1)=(a-b+1)(ab-c)
9)by²+4by-cy²-4cy-4c+4b=b(y²+4y+4)-c(y²+4y+4)=(y+2)²(b-c)
Докажите тождество:
4a^2 b^2(a^2+b^2)-(a^2+b^2)^3=(b^2-a^2)(a^4-b^4)
4a^2 b^2(a^2+b^2)-(a^2+b^2)^3=4a^4b^2+4a^2b^4-a^2-3a^4b^2-3a^2b^4-b^6=
=a^4b^2+a^2b^4-a^6-b^6=^2(a^4-b^4)-a^2(a^4-b^4)=(b^2-a^2)(a^4-b^4) ч.т.д.
y=Π/3-x
sin x+cos(Π/3-x)=1
sin x+cos Π/3*cos x+sin Π/3*sin x=1
sin x*(1+√3/2)+cos x*1/2=1
Переходим к половинным аргументам и умножаем все на 2.
2sin(x/2)*cos(x/2)*(2+√3) + cos^2(x/2) - sin^2(x/2) = 2cos^2(x/2)+2sin^2(x/2)
Переносимости все в одну сторону
3sin^2(x/2) - (4+2√3)*sin(x/2)*cos(x/2) + cos^2(x/2) = 0
Делим все на cos^2(x/2)
3tg^2(x/2)-(4+2√3)*tg(x/2)+1=0
Замена t=tg(x/2)
3t^2-(4+2√3)*t+1=0
Получили обычное квадратное уравнение
D/4=(2+√3)^2-3*1=4+4√3+3-3= 4+4√3
t1=tg(x/2)=[2+√3-√(4+4√3)]/3
t2=tg(x/2)=[2+√3+√(4+4√3)]/3
Соответственно
x1=2*arctg(t1)+Π*n; y1=Π/3-x1
x2=2*arctg(t2)+Π*n; y2=Π/3-x2
Уравнение не будет иметь решений, если .
.
ответ: