Квадратное уравнение может иметь один или два корня. Значит, из трёх чисел можно составить шесть приведённых (см. об этом ниже) уравнений: с корнями (2), (5), (9), (2; 5), (2; 9), (5; 9).
Составим уравнения с одним корнем — это будут полные квадраты:
Далее составим уравнения с двумя корнями. Используем теорему Виета: коэффициенты приведённого уравнения вычисляются по формулам .
Первое уравнение (2; 5):
Второе уравнение (2; 9):
Третье уравнение (5; 9):
ответ: шёсть приведённых уравнений:
А теперь рассмотрим неприведённые уравнения — в которых коэффициент при не равен единице (и нулю, конечно, поскольку тогда уравнение перестаёт быть квадратным).. Поскольку любое квадратное уравнение можно разложить на множители:
и в этом разложении при любом оно будет иметь те же корни, то таких уравнений можно составить бесконечное количество. Например, если взять уравнение и умножить его на любое число (кроме нуля): — то его корни останутся прежними.
Окончательный ответ: с данными корнями можно создать бесконечное количество неприведённых уравнений.
Квадратное уравнение может иметь один или два корня. Значит, из трёх чисел можно составить шесть приведённых (см. об этом ниже) уравнений: с корнями (2), (5), (9), (2; 5), (2; 9), (5; 9).
Составим уравнения с одним корнем — это будут полные квадраты:
Далее составим уравнения с двумя корнями. Используем теорему Виета: коэффициенты приведённого уравнения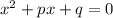 вычисляются по формулам
вычисляются по формулам 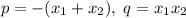 .
.
Первое уравнение (2; 5):
Второе уравнение (2; 9):
Третье уравнение (5; 9):
ответ: шёсть приведённых уравнений:
А теперь рассмотрим неприведённые уравнения — в которых коэффициент при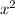 не равен единице (и нулю, конечно, поскольку тогда уравнение перестаёт быть квадратным).. Поскольку любое квадратное уравнение
не равен единице (и нулю, конечно, поскольку тогда уравнение перестаёт быть квадратным).. Поскольку любое квадратное уравнение 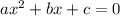 можно разложить на множители:
можно разложить на множители:
и в этом разложении при любом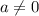 оно будет иметь те же корни, то таких уравнений можно составить бесконечное количество. Например, если взять уравнение
оно будет иметь те же корни, то таких уравнений можно составить бесконечное количество. Например, если взять уравнение 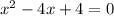 и умножить его на любое число (кроме нуля):
и умножить его на любое число (кроме нуля): 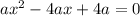 — то его корни останутся прежними.
— то его корни останутся прежними.
Окончательный ответ: с данными корнями можно создать бесконечное количество неприведённых уравнений.