task/29465133
√3sinx + cosx = 2
* * * методом вс угла: asinx + bcosx=√(a²+b²)sin(x+φ) , где
φ= arctg(b/a) || a =√3 ; b =1 ; √(a²+b²)= 2 ; φ= arctg(1/√3)=π/6 || * * *
но уравнение проще √3sinx + cosx = 2 ⇔ √3)/2 *sinx +(1/2)* cosx =1 ⇔
sinx*cos(π/6) +cosx*sin(π/6) =1 ⇔ sin(x +π/6) =1 ⇔x+π/6=π/2+2πn , n∈ ℤ .⇔
ответ : x =π/3+2πn , n∈ ℤ.
как не надо решать ( однородное уравнение)
* * * sin²α+cos²α=1 ; sin2α=2sinαcosα ; cos2α= cos²α - sin²α ; x =2*(x/2) * * *
√3sinx +cosx=2⇔2√3sin(x/2)cos(x/2)+cos²(x/2)-sin²(x/2)=2cos²(x/2)+2sin²(x/2)
⇔ 3sin²(x/2) -2√3sin(x/2)cos(x/2 +cos²(x/2) =0 || : cos²(x/2) ≠ 0
3tg²(x/2) - 2√3tg(x/2) +1 =0 кв. уравнение относительно tg(x/2) = t
D₁ =(√3)²-3*1=0 кратный корень
tg(x/2) = (√3)/3 * * * x /2 =arctg[(√3)/3] +πn , n ∈ ℤ * * *
tgx =tg[2*(x/2) ] = 2tg(x/2) / [ 1 - tg²(x/2) ] = √3 .
x = π / 3+ πn , n ∈ ℤ. откуда появился второй корень
4 < a < 7 и 3 < b < 5
1) а + b может ограничиваться 4+3 = 7; 4 + 5 = 9; 7 + 3 = 10; 7 + 5 = 12;
самое маленькое число 7, самое большое 12, поэтому
7 < а + b < 12
2) a/b ограничивается 4/3 ≈ 1,33; 4/5 = 0,8; 7/3 ≈ 2,33; 7/5 = 1,4;
нижняя граница 0,8, верхняя граница 2,33, поэтому
4/5 < a/b < 7/3
3) 2a - 5b - ?
8 < 2a < 14 и 15 < 5b < 25
2a - 5b ограничивается 8/15 ≈ 0.53; 8/25 = 0,32; 14/15 ≈ 0.93; 14/25 = 0.56;
нижняя граница 0,32, верхняя граница 0.93, поэтому
8/25 < 2a - 5b < 14/15
4) 4b/9a - ?
36 < 9a < 63 и 12 < 4b < 20
4b/9a ограничивается 12/36 ≈ 0,33; 12/63 = 4/21 ≈ 0,19; 20/36 = 5/9≈ 0,55; 20/63 ≈ 0,32;
нижняя граница 0,19, верхняя граница 0.55, поэтому
4/21 < 4b/9a < 5/9
5) (0.6b - 0.2a)/(0.7a - 0.1b)
0.8 < 0.2a < 1.4 и 1.8 < 0.6b < 3
0.6b - 0.2a - ограничивается 1.8 - 0.8 = 1; 3 - 0,8 = 2,2; 1,8 - 1,4 = 0,4; 3 - 1,4 = 1,6
нижняя граница 0,4; верхняя граница 2,2
0.4 < 0.6b - 0.2a < 2.2
2.8 < 0.7a < 4.9 и 0.3 < 0.1b < 0.5
0.7a - 0.1b ограничивается 2,8 - 0,3 = 2,5; 2,8 - 0,5 = 2,3; 4,9 - 0,3 = 4,6; 4,9 - 0,5 = 4,4
2.3 < 0.7a - 0.1b < 4.6
Рассмотрим (0.6b - 0.2a)/(0.7a - 0.1b)
0.4 < 0.6b - 0.2a < 2.2
2.3 < 0.7a - 0.1b < 4.6
(0.6b - 0.2a)/(0.7a - 0.1b) ограничивается 0,4/2,3 = 4/23 ≈ 0,17; 0,4/4,6 = 2/23 ≈ 0,09; 2,2/2,3 = 22/23 ≈ 0,96; 2,2/4,6 = 11/23 ≈ 0,48, поэтому
2/23 < (0.6b - 0.2a)/(0.7a - 0.1b) < 22/23
0.4 < 0.6b - 0.2a < 2.2
Объяснение:
Синус - это отношение противолежащего катета на гипотенузу.
Пусть противолежащий катет - 6, а гипотенуза - 11.
По теореме пифагора находим прилежащий катет -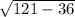
= 
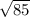
Находим косинус -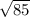
/11 и тангенс - 6/