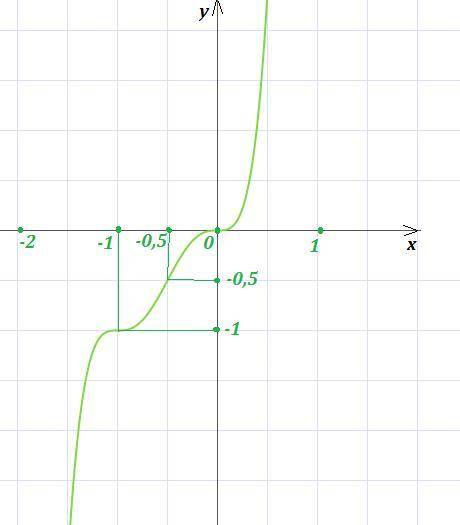
y=6x⁵+15x⁴+10x³
1) Область определения: х∈(-∞,+∞) .
2) Множество значений: у∈(-∞,+∞) .
3) Эта кривая не имеет асимптот, так как
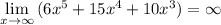 .
.
Нет точек разрыва.
4) Точка пересечения с осью ОУ (при х=0) одна - это (0,0).
5) Точка пересечения с осью ОХ тоже одна - (0,0) , так как
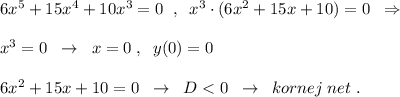
6) Интервалы монотонности и точки экстремума функции:
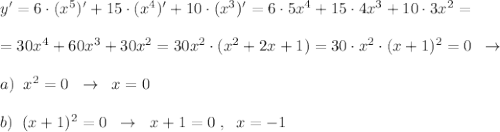
Подсчитаем знаки производной y' на полученных интервалах:
![+++[-1\, ]+++[\, 0\, ]+++](/tpl/images/3209/1216/1ee6c.png)
При переходе через точки х=0 и х= -1 производная не меняет знак, значит точки х=0 и х= -1 не являются точками экстремума. А на промежутках, где производная всюду положительна, сама функция возрастает.
Интервалы возрастания функции: x∈(-∞,-1 ]∪[-1,0 ]∪[0,+∞) .
7) Интервалы выпуклости и вогнутости, точки перегиба функции:
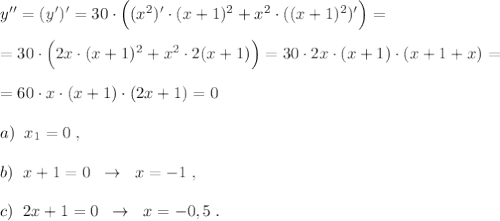
Определим знаки второй производной y'' на интервалах:
![---[-1\, ]+++[-0,5\, ]---[\, 0\, ]+++](/tpl/images/3209/1216/856a4.png)
На промежутках, где y''<0, функция y(x) выпукла, а там, где y''>0, функция вогнута. Точки перегиба - те точки, при переходе через которые у'' меняет знак,это х= -1 , х= -0,5 , х=0 .
8) Для более точного построения графика найдём координаты некоторых промежуточных точек: (-1,-1) , (-0,5 ; -0,5) .
График на рисунке.
Запишем формулу: P=m/n, где m – число исходов, благоприятствующих осуществлению события X, а n – число всех равновозможных элементарных исходов.
Для начала определим вероятность выпадения какого-либо числа при одном броске. Определённое число выпадает одно, а всего исходов может быть 6 (6 граней кубика). Значит, вероятность выпадения какого-либо числа = 1/6.
Так как бросков мы делаем 2, количество возможных результатов возводится во 2-ю степень, и вероятность выпадения какого-либо числа уже = 1 / 6 × 6 = 1/36. В последующем, мы будем домножать числитель на количество удовлетворяющих нас результатов.
Сумма выпавших очков делится на 5 при следующих результатах
1) 1 и 4 (=5)
2) 2 и 3 (=5)
3) 3 и 2 (=5)
4) 4 и 1 (=5)
5) 5 и 5 (=10)
Как видим, количество удовлетворяющих нас результатов = 5. Значит, вероятность выпадения числа, кратного 5 = 1 × 5 / 36 = 5/36 ≈ 0.139 = 13.9%
Сумма выпавших очков меньше, чем 8 при следующих результатах:
1) 1 и 1
2) 1 и 2
3) 1 и 3
4) 1 и 4
5) 1 и 5
6) 1 и 6
7) 2 и 1
8) 2 и 2
9) 2 и 3
10) 2 и 4
11) 2 и 5
12) 3 и 1
13) 3 и 2
14) 3 и 3
15) 3 и 4
16) 4 и 1
17) 4 и 2
18) 4 и 3
19) 5 и 1
20) 5 и 2
21) 6 и 1
Как видим, количество удовлетворяющих нас результатов = 21. Значит, вероятность выпадения чисел, сумма которых меньше 8 = 1 × 21 / 36 = 21/36 = 7/12 ≈ 0.583 = 58.3%
Произведение выпавших очков делится на 12 при следующих результатах:
1) 2 и 6
2) 3 и 4
3) 4 и 3
4) 6 и 2
Как видим, количество удовлетворяющих нас значений =4. Значит, вероятность выпадения чисел, произведение которых =12 составляет 1 × 4 / 36 = 4/36 = 1/9 ≈ 0,111 = 11,1%
Количество очков, выпавших в первый раз, и количество очков, выпавших
во второй раз, отличаются на 3 возможно при следующих результатах:
1) 1 и 4
2) 4 и 1
3) 2 и 5
4) 5 и 2
5) 3 и 6
6) 6 и 3
Как видим, количество удовлетворяющих нас результатов =6. Значит, вероятность выпадения чисел, количество очков которых, выпавших в первый раз, и количество очков, выпавших во второй раз, отличаются на 3 составляет 1 × 6 / 36 = 6/36 = 1/6 ≈ 0,166 = 16,6%
ответ: 1) 13.9%; 2) 58.3%; 3) 11,1%; 4) 16,6%.
320
Объяснение:
Так как степени корней одинаковые запишем их под один корень:
У нас получится:![\sqrt[6]{8^1^2 *5^6}](/tpl/images/1022/7246/b7c22.png)
Далее извлекаем корень, т.е. делим степень числа на степени корня 12/6 = 2 6/6 = 1, получается: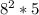
Далее возводим 8 в квадрат - это 8*8 = 64 и умножаем на 5, получается 320