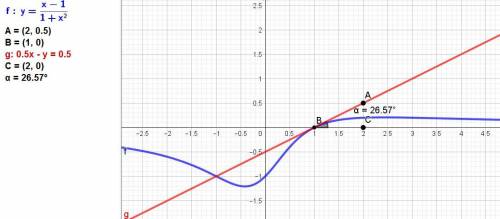
1) Находим точку пересечения кривой с осью абсцисс.
х - 0 = 0, отсюда х = 1.
Производная заданной функции y'(x) = (-x²+2*x+1)/(1+x²)².
В точке х = 1 значение производной y'(1) = (1/2).
Угол наклона касательной равен:
α = arc tg(1/2) = 0,464 радиан или 26,565 градуса.
2) Даны парабола y= х² и прямая р: 2x-6y+5=0.
Перпендикуляр к касательной к параболе- это нормаль:
y = (1/y'(x0) - x0) + y0.
Угловой коэффициент такой нормали равен: к = -1/к(р).
У прямой р к(р) = 2/6 = 1/3, тогда к = -1/(1/3) = -3.
Приравниваем -3 = (1/y'(x0), y'(x0) = -3.
Производная функции y = x² равна: y' = 2x.
Приравняем 2х = -3, откуда х = -3/2 а у = (-3/2)² = 9/4.
ответ: точка ((-3/2); (9/4)).
пересекает ось абсцисс2) в ка" />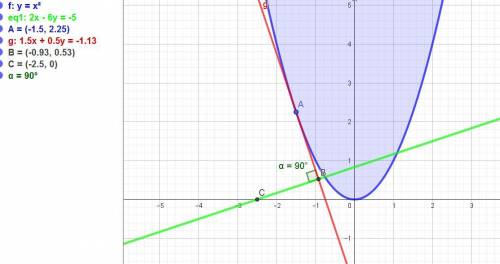
пересекает ось абсцисс2) в ка" />
task/29760192 cos(3x/2)*cos(x/2) -1 > (1/2) * (1 -√3) *cosx
Решение : cos(3x/2)*cos(x/2) -1 > (1/2) * (1 -√3) *cosx ||*2||
2cos(3x/2)*cos(x/2) -2 > (1 -√3) *cosx ;
cos2x+cosx - (1 -√3) *cosx - 2 > 0 ;
2cos²x -1 +cosx - cosx +(√3) *cosx - 2 > 0 ;
2cos²x +(√3) *cosx -3 >0 ⇔ ( cosx +√3 )(2cosx -√3 ) >0 ||cosx +√3 >0 ||⇔ cosx > (√3) /2 ⇒ 2πn - π / 6 < x < π / 6 + 2πn , n ∈ ℤ (объединение интервалов )
ответ : x ∈ ( - π / 6 + 2πn ; π / 6 + 2πn ) , n ∈ ℤ.
P.S. 2cos²x +(√3) *cosx -3 = 0. D=(√3)²+4*2*(-3) =27 =(3√3)² ⇒√D =3√3)
cosx₁ = - √3 < - 1 → посторонний корень ; cosx₂ =(√3) / 2. * * *
2222 - 111 - 99 + 5 = 2017.
Посмотрим, чему может равняться число . Так как выражение "- EEE - AA + R" больше или равно - 1086 (= - 999 - 88 + 1), то должно быть довольно близко к 2017. 3333 и 1111 не подходят, значит = 2222.
Теперь обратим внимание на число EEE. Пусть оно равно 222 или больше. Тогда у нас получится 2222 - 222 = 2000 или меньше. Теперь от этого числа нужно отнять некоторое двузначное и прибавить однозначное, то есть еще уменьшить число. Но так невозможно будет получить 2017. Значит, EEE = 111.
Мы имеем: 2222 - 111 = 2111. Если мы отнимем 94, то получим ровно 2017, но тогда R = 0 (ненатуральное). Тогда мы можем подставить A = 95, 96, 97, 98, 99 и получим соответственно R = 1, 2, 3, 4, 5. Но А должно состоять из одной цифры, так что A = 99, R = 5.
Примечание:
При решении ребуса мы учитывали то, что все числа являются натуральными, и не повторяются (то есть Y не может быть равно R и т. д.).
ответ: 1) α=arctg(1/2)≈-26,6°. 2) M(-3/2;9/4).
Объяснение:
1) Угол, под которым кривая пересекает ось абсцисс, есть угол наклона касательной, проведённой к графику функции в точке пересечения, к оси абсцисс. Решая уравнение y=0, находим x=1 - абсцисса точки пересечения кривой с осью абсцисс. Сама точка пересечения имеет координаты (1;0). Пусть α - искомый угол, тогда tg(α)=y'(x0), где x0=1 - абсцисса точки пересечения кривой с осью абсцисс. Находим производную: y'(x)=(-x²+2*x+1)/(1+x²)². Отсюда y'(x0)=y'(1)=1/2. Тогда α=arctg(1/2)≈26,6°.
2) Пусть M(x0;y0) - искомая точка. Перепишем уравнение прямой в виде y=1/3*x+5/6. Отсюда следует, что угловой коэффициент этой прямой k1=1/3. Пусть k2 - угловой коэффициент касательной. Так как по условию она перпендикулярна данной прямой, то k2=-1/k1=-3. Но k2=y'(x0). Находим производную: y'=2*x, тогда y'(x0)=2*x0 и отсюда следует уравнение 2*x0=k2=-3. Решая его, находим x0=-3/2, а тогда y0=x0²=9/4. Таким образом, точка М найдена.