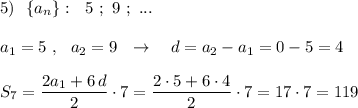

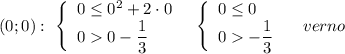
Для других точек хотя бы одно неравенство будет неверным.
Например,
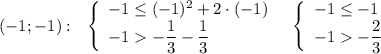 неверно 2 неравенство
неверно 2 неравенство
7) Из города А в город В ведут 8 дорог. Обозначим их: 1,2,3,4,5,6,7,8 .
Из города В в город С ведут 9 дорог. Обозначим их: a,b,c,d,e,f,g,i,k .
Тогда можно написать, какие маршруты могут быть.
(1,a) (1,b) (1,c) (1,d) (1,e) (1,f) (1,g) (1,i) (1,k)
(2,a) (2,b) .......................................................... (2,k)
(3,a) (3,b)............................................................. (3,k)
........................................................................................
(8,a) (8,b).............................................................. (8,k)
Образовалась таблица из 8 строчек и 9 столбцов. Количество элементов в этой таблице равно 8*9=72 . Поэтому и маршрутов может быть 72 .
y = - x³ + 3x² + 4
Найдём производную :
y' = (- x³)' + 3(x²)' + 4' = - 3x² + 6x
Приравняем производную к нулю , найдём критические точки :
- 3x² + 6x = 0
- 3x(x - 2) = 0
x₁ = 0
x - 2 = 0 ⇒ x₂ = 2
Обе критические точки принадлежат заданному отрезку. Найдём значения функции в критических точках и на концах отрезка и сравним их .
y(- 3) = -(- 3)³ + 3 * (- 3)² + 4 = 27 + 27 + 4 = 58
y( 3) = - 3³ + 3 * 3² + 4 = - 27 + 27 + 4 = 4
y( 0) = - 0³ + 3 * 0² + 4 = 4
y(2) = - 2³ + 3 * 2² + 4 = - 8 + 12 + 4 = 8
Наименьшее значение функции равно 4, а наибольшее равно 58 .
Разложить на множители.