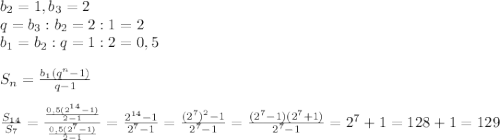
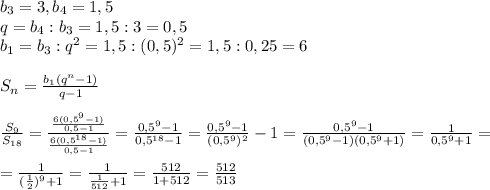
Функция не имеет промежутков убывания
Объяснение:
По теореме если угловой коэффициент прямой меньше нуля, то функция убывает, а если угловой коэффициент прямой больше нуля, то функция возрастает.
Докажем теорему
Рассмотрим функцию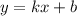 
.Где x,y - переменные; k,b - параметры. Продифференцируем функцию y.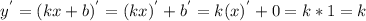
По теореме если производная больше нуля на промежутке M, то на этом промежутке функция возрастает.
По теореме если производная меньше нуля на промежутке M, то на этом промежутке функция убывает.
Тогда согласно теоремам:
если k < 0, то функция убывает.
если k > 0, то функция возрастает.
y=2x − 4 ⇒ k > 0, тогда функция возрастает при x є R.
1)Найдём абсциссу точки пересечения графиков этих из уравнения
f(x) = g(x)
2 √x = 2√(6-x) - возводим в квадрат обе части
4х = 4(6-x)
4х = 24 - 4х
8х = 24
х = 3
Угол, под которым пересекаются графики - это угол между касательными, проведёнными к линиям в точке их пересечения. Производная функции в данной точке равна угловому коэффициенту касательной, проведённой к графику функции в данной точке, поэтому угол, под которым пересекаются линии, находимм по формуле:
tgα = (k₁ - k₂)/(1 +k₁k₂)
k₁ = f'(x₀), k₂ = g'(x₀)
Сначала найдем значения производных функций в точке х = 3:
f'(x) = (2 √x)' = 1/√x k₁ = f'(3) = 1/√3
g'(x) = (2√(6-x))' = - 1/√6-x k₂ = g'(3) = - 1/√6-3 = - 1/√3
Тогда тангенс угла пересечения в точке х = 1 равен
tgα = (1/√3 - (- 1/√3)) / (1 + 1/√3*(- 1/√3)) = 2/√3 / (1 - 1/3) =
= 2/√3 : 2/3 = 2/√3 * 3/2 = √3
=> α = arctg √3 = π/3
ответ: графики функций углом пересекаются углом пересекаются пересекаются под углом π/3.
