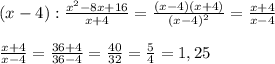
5/4
Объяснение:
(x-4):((x^2-8*x+16)/(x+4))=(x-4):((x-4)^2/(x+4))
=(x-4)*(x+4)/(x-4)^2=(x+4)/(x-4)=(36+4)/(36-4)
=40/32=5/4
Функция
- убывает на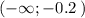 
- возрастает на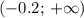 
Точка минимума функции:
x = -0.2
Объяснение:
Функция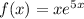 
определена на R, или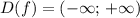 
Для нахождения промежутков возрастания (убывание) и точек экстремума находим производную функции f'(x):
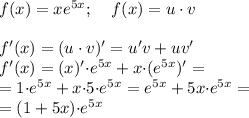
Производная исследуемой функции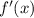 
также определена на R, или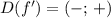 
Найдем критические точки
Т.к. производная исследуемой функции 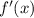также определена на R, или 
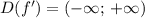, найдем нули производной :
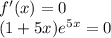
что равносильно совокупности:
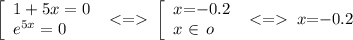
Найдем промежутки возрастания / убывания:
Функция возрастает при f'(x) > 0
убывает при f'(x) < 0
Для этого исследуем точку x = -0,2 на экстремум: знак производной
- при х < -0.2 f'(x) < 0 => функция f(x)
убывает на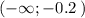
- при х > -0.2 f'(x) < 0 => функция f(x)
возрастает на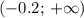
В точке x = -0.2 происходит смена функции
с убывания --> на возрастание
Следовательно, x = -0.2 - является единственной точкой экстремума, а именно это - точка минимума функции
