1.
a)
x² + 4x + 10 ≥ 0
Рассмотрим функцию у = x² + 4x + 10.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 4x + 10 = 0
D = 16 - 40 = - 24 < 0
нулей нет, значит график не пересекает ось Ох.
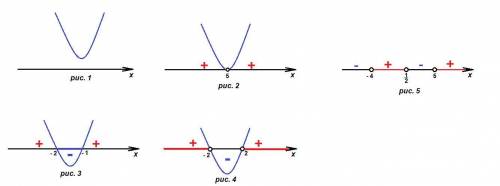
Схематически график изображен на рис. 1.
у > 0 при x ∈ (- ∞; + ∞)
ответ: 2) Решением неравенства является вся числовая прямая.
b)
- x² + 10x - 25 > 0 | · (- 1)
x² - 10x + 25 < 0
Рассмотрим функцию у = x² - 10x + 25.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 10x + 25 = 0
(x - 5)² = 0
x = 5
Схематически график изображен на рис. 2.
у < 0 при x ∈ {∅}
ответ: 1) Неравенство не имеет решений.
c)
x² + 3x + 2 ≤ 0
Рассмотрим функцию у = x² + 3x + 2.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² + 3x + 2 = 0
D = 9 - 8 = 1
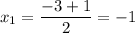
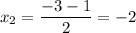
Схематически график изображен на рис. 3.
у ≤ 0 при x ∈ [- 2; - 1]
ответ: 4) Решением неравенства является закрытый промежуток.
d)
- x² + 4 < 0 | · (- 1)
x² - 4 > 0
Рассмотрим функцию у = x² - 4.
Функция квадратичная, график - парабола, ветви направлены вверх.
Нули функции:
x² - 4 = 0
x² = 4
x = ± 2
Схематически график изображен на рис. 4.
у > 0 при x ∈ (- ∞; - 2) ∪ (2; + ∞)
ответ: 6) Решением неравенства является объединение двух промежутков.
___________________________
2.
(x - a)(2x - 1)(x + b) > 0
x ∈(- 4; 1/2) ∪ (5; + ∞)
Решение неравенства показано на рис. 5.
Найдем нули функции у = (x - a)(2x - 1)(x + b).
(x - a)(2x - 1)(x + b) = 0
(x - a) = 0 или (2x - 1) = 0 или (x + b) = 0
x = a x = 1/2 x = - b
Из решения неравенства следует, что нулями являются числа - 4, 1/2 и 5. Значит
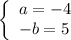 или
или 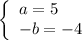
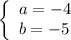 или
или 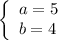
ответ: a = - 4, b = - 5 или a = 5, b = 4.
Используя то,что |a-b|=|b-a| получим:
|5x-13|-|5x-6|=7
Найдем корни(нули) подмодульных выражений:
5x-13=0 =>x=2,6
5x-6=0 => x=1,2
Отметим эти точки на оси:
1,22,6
Эти числа разбивают ось на три промежутка.Рассмотрим все 3 случая:
1)x<=1,2
Оба подмодульных выражения отрицательны на этом промежутке, поэтому раскроем модули со сменой знака:
-5x+13+5x-6=7
7=7
Это означает, что весь числовой промежуток является решением уравнения.
2)1,2<x<=2,6
Первый модуль мы раскроем со сменой знака, второй - без смены знака:
-5x+13-5x+6=7
-10x+19=7
-10x=-12
x=1,2 - корень не входит в рассматриваемый промежуток,но он входит в предыдущий промежуток.
3)x>=2,6
Оба модуля раскроем без смены знака:
5x-13-5x+6=7
-7=7
На этом промежутке у нас пустое множество.
Вывод: решением уравнения является промежуток x<=1,2. Наибольшее целое решение из этого промежутка = 1.
ответ:1