ответ:с графиком)
Объяснение:
а) 3 прямые имеют наибольшее число точек пересечения 3 ,
б) 4 прямые - 6 точек пересечения ,
в) 5 прямых - 10 точек пересечения ,
г) n прямых - \frac{n(n-1)}{2}
2
n(n−1)
точек пересечения .
Решение. Заметим, что наибольшее число точек попарных пересечений получается, если каждая прямая пересекается с каждой и при этом никакие три прямые не пересекаются в одной точке. В этом случае количество точек попарных пересечений равно количеству пар прямых из данного множества n прямых. Как мы знаем, это число равно \frac{n(n-1)}{2}
2
n(n−1)
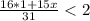
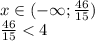то есть да может , так как 
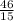ее целая часть равна 3 , а она натуральное число , и найдется набор таких чисел что среднее арифметическое будет меньше 2 , так как в условий не сказано что , сам набор может состоят так только из разных натуральных чисел. 
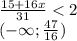, целая часть этого числа равна 
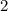, то есть не может , так как в сумме 
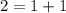, и по количеству в этом наборе минимальное есть 16 единиц . 
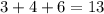так как мы ранее доказали что , есть не менее 16 единиц , и того 
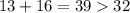что удовлетворяет условию .
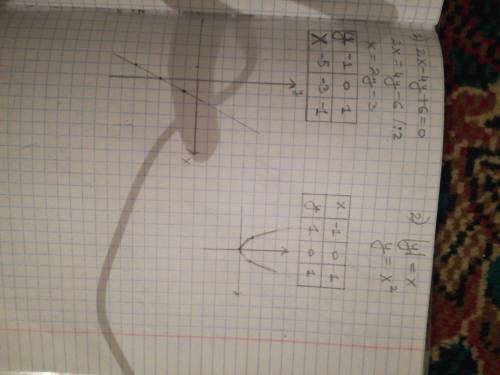
х=2у-3
Объяснение:
2х-4у+6=0
2х=4у-6
х=2у-3