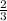 от того, что осталось после первого деня, то после второго дня работы осталась
от того, что осталось после первого деня, то после второго дня работы осталась  от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно
от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно  =2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
=2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
Разложим на множители 24:
Чтобы число делилось на 24, оно должно одновременно делиться на 8 и на 3.
Чтобы число делилось на 8, то число, составленное из трёх последних цифр, должно делиться на 8. Простым перебором найдём, что таким числом является только 544. Значит, последние три цифры — 544.
Чтобы число делилось на 3, сумма его цифр должна делиться на 3. Сумма последних трёх цифр равна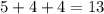 . Вариантов первых трёх цифр четыре: 445, 455, 444, 555 (порядок цифр здесь уже не важен). Проверим каждый из вариантов:
. Вариантов первых трёх цифр четыре: 445, 455, 444, 555 (порядок цифр здесь уже не важен). Проверим каждый из вариантов:
Видим, что сумма цифр делится на 3, если первые три цифры 455 (в любом порядке). Тогда их можно расположить в таком порядке: либо 455, либо 545, либо 554.
ответ. Подходят три числа: