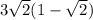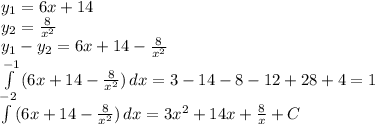
ответ: ymin=y(-4)=-164
Объяснение:
Найдите наименьшее значение функции у = х³ - 5х² + 8х + 12 на отрезке [-4;1].
Найдем значение функции на границах отрезка
у(-4) = (-4)³ - 5·(-4)² +8·(-4) + 12 = -64 - 80 - 32 + 12 = -164
у(1) = 1³ - 5·1² +8·1 + 12 = 1 - 5 + 8 + 12 = 16
Найдем производную функции
у' =(х³ - 5х² + 8х + 12)' = (х³)' - (5х²)' + (8х)' + (12)' = 3x² - 10x +8
Найдем критические точки приравняв производную к нулю
3x² - 10x + 8 = 0
D = (-10)² - 4·3·8 = 100 - 96 = 4
x₁ = (10-2)/(2·3) = 8/6 = 4/3 ≈ 1,33
x₂ = (10+2)/(2·3) = 12/6 = 2
Найденные точки не входят в данный отрезок поэтому значения функции в них находить не будем.
Функция на отрезке монотонна и возрастает. Минимальное значение функции находится в точке x = -4 y(-4) = -164
![РЕШИТЬ.Найдите наименьшее значение функции у=х^3-5х^2+8х+12 на отрезке [-4;1].](/tpl/images/1353/3405/90f6a.jpg)
Объяснение:
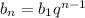решаем по этой формуле (1)
q - знаменник
131 - 1) 32 = 108q³ ⇒ q³ = 8/27 ⇒ q = 2/3
131-2) b₃ = 
⇒ q = √5
132. 7-4 = 3 ⇒ c₇ = c₄*q³ ⇒ q³ = -320/40 = -8 ⇒ q = -2 ⇒ c₁ = c₄/q³ = 40/8 = 5
133. b₁ = 3/4, q = 2
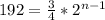
n-1 = 8
n = 9
134. 48, 48q, 48q², 48q³, 243 ⇒ 243 = 48q⁴ ⇒ q⁴ = 243/48 = 81/16 ⇒ q = 3/2 = 1.5
48, 72, 108, 162, 243 вот жирным выделены эти ТРИ числа
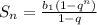(2)
135-1) из ф-лы (1): 280= b₁5³ ⇒ b₁ = 280/125 = 56/25
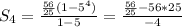
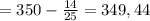
135-2) из формулы (1) 4√2 = q⁴ *√2 ⇒ q = -√2 Т. к. по условию q <0
из (2)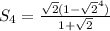 
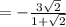или 
