1) проверяем условие при наименьшем возможном значении n.
n>5, значит проверяем условие при n=6
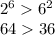
Верно!
2) Сделаем предположение, что для всех n=k, k>5 верно неравенство:
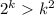
3) Тогда при n=k+1 должно выполняться неравенство:
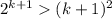
Вернемся к неравенству из второго пункта и домножим его на 2:
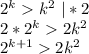
Подставим 2k² в 3-й пункт и рассмотрим полученное неравенство:
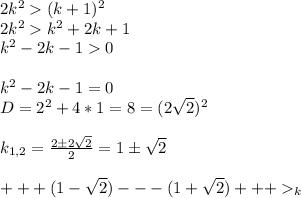
по методу интервалов определяем, что неравенство k²-2k-1>0 выполняется при k>1+√2, тогда при k>5 оно тоже выполняется (так как 5>1+√2)
Тогда обратным ходом получаем 2k²>k²+2k+1 при k>5 или 2k²>(k+1)² при k>5
Если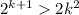 
, а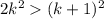 
, при k>5
То есть,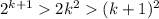 
, при k>5, то по закону транзитивности:
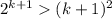, при k>5 - ч.т.д
Задание 4.
В задании явно видна развернутая формула суммы кубов, которую, для удобства, можно свернуть
Сумма кубов -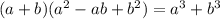 
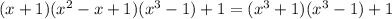
Теперь просто раскрываем скобки (можно воспользоваться формулой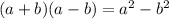 
, но при этом надо знать что x будет в степени 3 · 2; чтобы не усложнять решение и не запутывать его, раскрою скобки не по формуле)
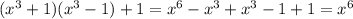
ответ: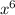 
.
Задание 5.
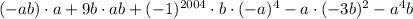
Если степень чётная, то числа в этой скобке при раскрытии, даже со знаком минус, становятся положительным и в степени, стоявшей после скобки.
Таким образом, (-ab) будет иметь нечётную (первую) степень и раскроется как -ab;
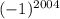будет иметь четную степень и раскроется как 1 (при умножении 1 на любое кол-во раз получается 1);
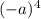будет иметь четную степень и раскроется как 
;
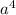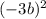раскроется как 
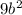(мы умножаем каждую букву и число в скобке)
Получаем
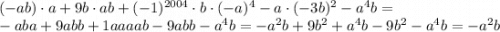
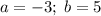
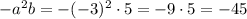
ответ: -45.
