 побудувати графік функ" />
побудувати графік функ" />
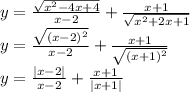
Возможны несколько вариантов:
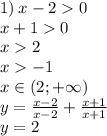
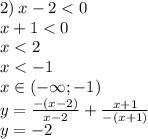
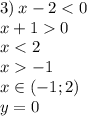
Остаётся просто построить прямые на плоскости операясь на наши органичения.
 побудувати графік функ" />
побудувати графік функ" />
1) В таблицах значений.
2)Да, проходит.
Объяснение:
1) Построить график функции y = -3x + 6.
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
y = -3x + 6
Таблица:
х -1 0 1
у 9 6 3
2) Выяснить, проходит ли график функции через точку M(-20; 66)
Чтобы определить принадлежность точки графику, нужно известные значения х и у (координаты точки) подставить в уравнение, если левая часть будет равна правой, значит, точка принадлежит графику и наоборот.
M(-20; 66) y = -3x + 6
66= -3*(-20)+6
66= 60+6
66=66, проходит.
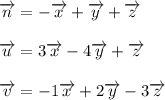
В базисе  векторы имеют следующие координаты:
векторы имеют следующие координаты:
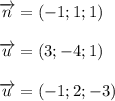
Их координаты попарно не пропорциональны, поэтому эти векторы не коллинеарны между собой.
Докажем компланарность векторов двумя
школьный (≈10 класс)
Признак компланарности трёх векторов:
Пусть векторы 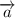 и
и 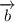 не коллинеарны. Если для вектора
не коллинеарны. Если для вектора 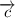 существует единственная пара реальных чисел A и B, такая, что
существует единственная пара реальных чисел A и B, такая, что 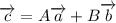 , то векторы
, то векторы 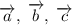 компланарны.
компланарны.
Покажем, что
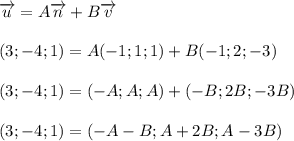
Слева и справа стоят координаты векторов. Векторы равны, если равны их соответственные координаты:
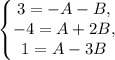
Сложим первое и второе уравнение, получим:
-1 = B
Подставим значение B в первое уравнение, найдём A:
3 = -A - (-1)
A = -2
Проверим найденные значения для остальных уравнений системы.
Итого получаем:
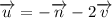
То есть признак выполнен. Значит векторы компланарны.
обычно проходится в вузах):
Векторы 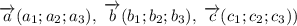 компланарны, если
компланарны, если
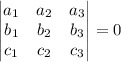
Проверим это условие для данных векторов:
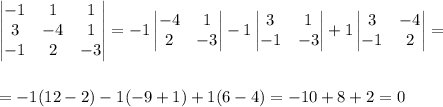
Следовательно, векторы компланарны.