14 см
Объяснение:
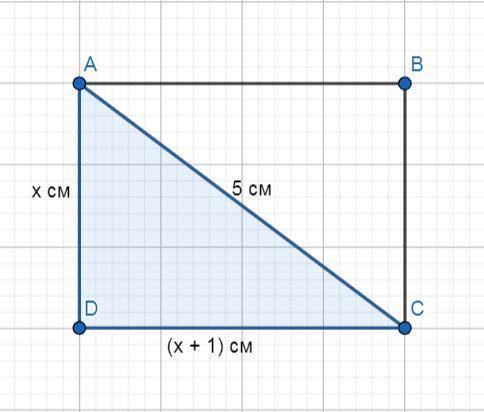
Рассмотрим ΔADC: ∠D = 90° (т.к. у прямоугольника все углы прямые); АС = 5 см
т. Пифагора (c² = a² + b²)
AC² = AD² + DC²
→ Пусть AD = х см, тогда DC = (х + 1) см.
5² = х² + (х + 1)²
х² + х² + 2х + 1 = 25
2х² + 2х - 24 = 0 |:2
х² + х - 12 = 0
а = 1; b = 1; с = -12 (формулу см. в первом вложении)
D = 1² - 4 * 1 * (-12) = 1 + 48 = 49 = 7²
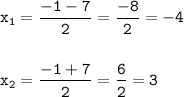
т.к. сторона не может быть отрицательна, то
AD = 3 см
DC = 3 + 1 = 4 см
******************
P прямоугольника = (a + b) * 2, где а,b - стороны прямоугольника
(3 + 4) * 2 = 14 см - периметр данного прямоугольника
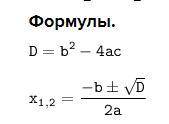
2 - 2x >= 5x - 3 - 2
-7x>=-7
x<=1
2) 7x+3>5(x-4)+1
7x + 3 > 5x - 20 + 1
2x > -22
x>-11
3) x^2-9>0
x^2 > 9
x>3
or
x<-3
4) x^2-11x+30<=0
D = 121 - 120 = 1
x1 = (11+1)/2 = 6 => x <= 6
x2 = (11-1)/2= 5 => x>=5 => 5<=x<=6
5) -2x^2+5x-2<0
D = 25 - 16 =9
x1 = (-5+3)/(-4) = 0,5 => x<0,5
x2 = (-5-3)/(-4) = 2 => x>2
6) (2x+3)(x-1)<0
{+} {+}
oo>x
-1,5 {-} 1
-1,5<x<1
7) x(4-x)(x+1)>=0
{+} {+}
|||>x
-1 {-} 0 4 {-}
x<=-1 and 0 <= x <=4
8) (2x-4)/(-x+5)>=0
{+} {+}
o|>x
-5 {-} 2
-5 < x <= 2