y = x⁴ - 2x²
Чтобы найти экстремумы, для начала нам нужно найти производную, а потом приравнять её к нулю, решив уравнение:
y' = (x⁴ - 2x²)' = (x⁴)' - (2x²)' = 4 · x⁴⁻¹ - 2 · 2 · x²⁻¹ = 4x³ - 4x
y' = 0, тогда:
4x³ - 4x = 0
4x · (x² - 1) = 0 в том случае, когда:
1. 4x = 0
x = 0
2. x² - 1 = 0
x² = 1
x = ± 1
Проведём числовую прямую и по методу интервалов определим, на каких промежутках значение функции положительно, а где отрицательно:
(смотри рисунок)
Чтобы определить знак функции на определённом промежутке, нужно подставить какое-то значение из этого промежутка в производную.
Точки экстремума - это точки максимума и минимума. Точка максимума - это точка, до которой график функции возрастал, а после этой точки убывал. Точка минимум - наоборот. На нашей числовой прямой таких экстремумов 3:
x₁ = -1 (минимум)x₂ = 0 (максимум)x₃ = 1 (минимум)Найдём значение функции в этих точках:
y(x₁) = x₁⁴ - 2x₁² = 1 - 2 = -1y(x₂) = x₂⁴ - 2x₂² = 0y(x₃) = x₃⁴ - 2x₃² = 1 - 2 = -1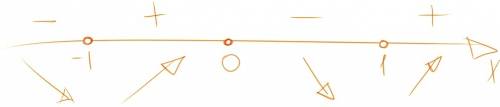
8 изначально, 9 после ускорения.
Объяснение:
Представим заказ за y, а ежедневную норму как x и получаем уравнения:
20x=y;
18(x+1) = y + 2;
Раскроем скобки 2го уравнения:
18x + 18 = y + 2;
Перенесем 12 через знак равенства и получим:
18x + 18 + (-2) = y;
18x + 16 = y;
Получаем систему уравнений:
20x = y;
18x + 16 = y;
Подставим первую часть любого уравнения во вторую часть другого уравнения:
18x + 16 = 20x;
18x + 16 + (-20x) = 0;
-2x + 16 = 0;
-2x = -16
x = (-16) / (-2) = 8
Изначально он делал 8, но если надо найти сколько он выполнил при ускорении работы то прибавим к ответу 1:
8 + 1 = 9.