Решение методом разложения:
Разложим числа на простые множители и подчеркнем общие множители чисел:
58110697294650 = 2 · 3 · 3 · 3 · 5 · 5 · 7 · 7 · 7 · 11 · 11 · 13 · 13 · 17 · 19 · 19
3191270940 = 2 · 2 · 3 · 3 · 3 · 5 · 11 · 11 · 13 · 13 · 17 · 17
Общие множители чисел: 2; 3; 3; 3; 5; 11; 11; 13; 13; 17
Чтобы найти НОД чисел, необходимо перемножить их общие множители:
НОД обоих чисел = 2 · 3 · 3 · 3 · 5 · 11 · 11 · 13 · 13 · 17 = 93860910
Решение методом Евклида:
1) 58110697294650 : 3191270940 = 18209 (ост. 844748190)
2) 3191270940 : 844748190 = 3 (ост. 657026370)
3) 844748190 : 657026370 = 1 (ост. 187721820)
4) 657026370 : 187721820 = 3 (ост. 93860910)
5) 187721820 : 93860910 = 2 без остатка.
Значит, 93860910 является НОД.
Примечание:
Проверку прикрепил фотографией.
ответ: НОД = 93860910.
функция 
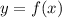не существует. То есть найдем такие значения , при которых выражение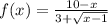 
не имеет смысла. Посмотрели на выражение, подумали и прикинули, что тут может быть где-то два варианта, при которых выражение не имеет смысла:
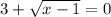, однако понятно, что 
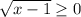, значит знаменатель не обратиться в нуль.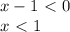
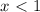функции не существует. То есть она идет от 
и куда-то дальше. Куда — нам пока неизвестно. . Может быть она периодична?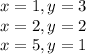 
, при котором числитель обратиться в нуль.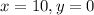 
повставлять разные значения (большие и маленькие). 
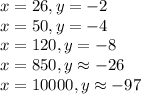
уменьшается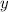 
. Делаем вывод, что функция убывает бесконечно много. То есть 
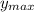— не существует, 
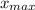— не существует.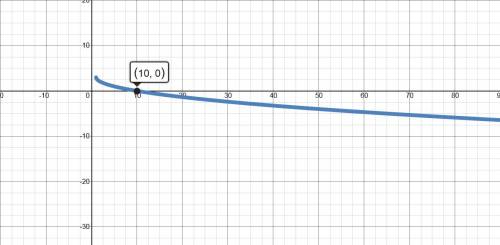 
Объяснение:
надо найти (х1+х2)/2
по т. Виета
х1+х2=-в (из первого уравнения)
(х1+1+х2+1)=в (из второго уравнения)
сложим каждую часть
х1+х2+х1+1+х2+1=0
2х1+2х2=-2
х1+х2=-1
(х1+х2)/2= -1/2