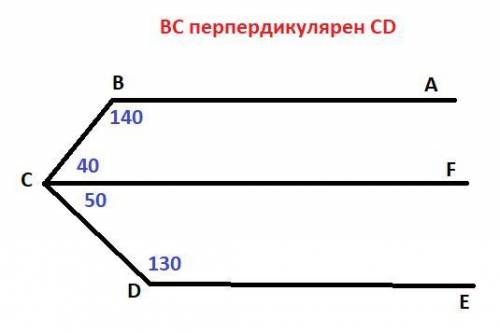
Условие: BA║DE, ∠CBA = 140°, ∠CDE = 130°. Доказать, что BC⊥CD.
Дано: BA║DE, ∠CBA = 140°, ∠CDE = 130°.
Доказать: BC⊥CD.
Доказательство:
Проведем из точки С прямую CF, параллельную прямым BA и DE.
∠CBA и ∠BCF - односторонние углы при BA║CF и секущей ВС.∠DCF и ∠CDE - односторонние углы при CF║DE и секущей CD.Сумма односторонних углов при параллельных прямых и секущей равна 180° ⇒
∠CBA + ∠BCF = 180°
∠DCF + ∠CDE = 180°
∠BCF = 180° - ∠CBA = 180° - 140° = 40°∠DCF = 180° - ∠CDE = 180° - 130° = 50°∠BCD = ∠BCF + ∠DCF = 40° + 50° = 90°
Значит, BC⊥CD, что и требовалось доказать.
1.(x+2)(x-3)-(2x-5)(x+3)=x(x-5)
х2-3х+2х-6-2х2-6х+5х+15=х2-5х
х2-3х+2х-6-2х2-6х+5х+15-х2+5х=0
-2х2+3х+9=0
Д=9+4*(-2)*9=0
х1=-3+9/-4=-1,5
х2=-3-9/-4=3
2.(6х-5)2+(3х-2)(3х+2)=36
36х2-25+9х2-4=36
45х2-29-36=0
45х2=65
х2=65/45=1,44
х=корень 1,44=1,2
Объяснение: