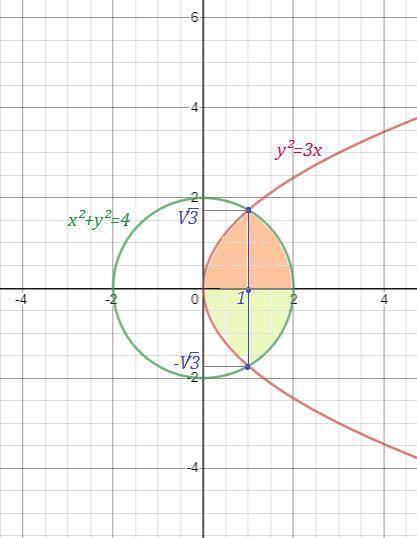
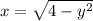 - это правая полуокружность от окружности
- это правая полуокружность от окружности 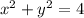 с центром в точке (0,0) и R=2 , выразим
с центром в точке (0,0) и R=2 , выразим 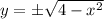 , причём для 1-ой четверти знак перед корнем (+) , а для 4-ой четверти знак (-) .
, причём для 1-ой четверти знак перед корнем (+) , а для 4-ой четверти знак (-) .
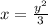 - это парабола , ветви которой направлены вправо, вершина в точке (0,0) . Выразим y:
- это парабола , ветви которой направлены вправо, вершина в точке (0,0) . Выразим y: 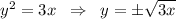 , причём знак (+) перед корнем для 1-ой четверти, а знак (-) для 4-ой четверти.
, причём знак (+) перед корнем для 1-ой четверти, а знак (-) для 4-ой четверти.
Область симметричная относительно оси ОХ. Поэтому можно подсчитать площадь одной половины, а затем удвоить её.
Найдём точки пересечения окружности и параболы.
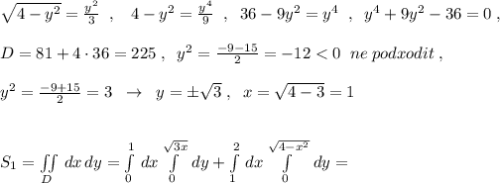
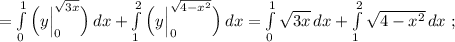
![Q=\int \sqrt{4-x^2}\, dx\\\\Q=\int \frac{4-x^2}{\sqrt{4-x^2}}\, dx=4\int \frac{dx}{\sqrt{4-x^2}}-\int \frac{x\, \cdot \, x\, dx}{\sqrt{4-x^2}}=\Big[\; u=x\; ,\; du=dx\; ,\\\\dv=\frac{x\, dx}{\sqrt{4-x^2}}\; ,\; v=-\frac{1}{2}\cdot 2\sqrt{4-x^2}=-\sqrt{4-x^2}\; ,\; \int u\, dv=uv-\int v\, du\; \Big]=\\\\=4\cdot arcsin\frac{x}{2}-\Big(-x\sqrt{4-x^2}+\int \sqrt{4-x^2}\, dx\Big)=\\\\=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}-Q\; \Rightarrow \; \; Q=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}-Q\; ,](/tpl/images/1075/2260/84be5.png)
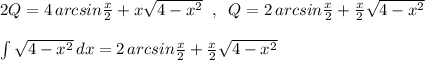
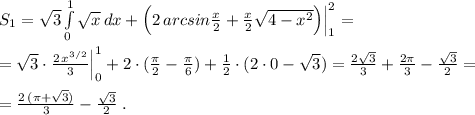
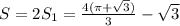
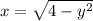 - это правая полуокружность от окружности
- это правая полуокружность от окружности 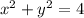 с центром в точке (0,0) и R=2 , выразим
с центром в точке (0,0) и R=2 , выразим 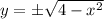 , причём для 1-ой четверти знак перед корнем (+) , а для 4-ой четверти знак (-) .
, причём для 1-ой четверти знак перед корнем (+) , а для 4-ой четверти знак (-) .
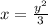 - это парабола , ветви которой направлены вправо, вершина в точке (0,0) . Выразим y:
- это парабола , ветви которой направлены вправо, вершина в точке (0,0) . Выразим y: 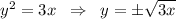 , причём знак (+) перед корнем для 1-ой четверти, а знак (-) для 4-ой четверти.
, причём знак (+) перед корнем для 1-ой четверти, а знак (-) для 4-ой четверти.
Область симметричная относительно оси ОХ. Поэтому можно подсчитать площадь одной половины, а затем удвоить её.
Найдём точки пересечения окружности и параболы.
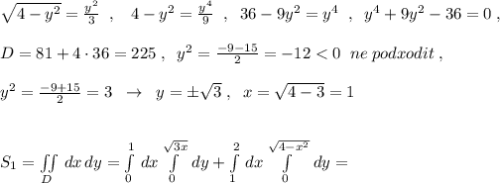
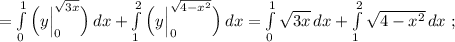
![Q=\int \sqrt{4-x^2}\, dx\\\\Q=\int \frac{4-x^2}{\sqrt{4-x^2}}\, dx=4\int \frac{dx}{\sqrt{4-x^2}}-\int \frac{x\, \cdot \, x\, dx}{\sqrt{4-x^2}}=\Big[\; u=x\; ,\; du=dx\; ,\\\\dv=\frac{x\, dx}{\sqrt{4-x^2}}\; ,\; v=-\frac{1}{2}\cdot 2\sqrt{4-x^2}=-\sqrt{4-x^2}\; ,\; \int u\, dv=uv-\int v\, du\; \Big]=\\\\=4\cdot arcsin\frac{x}{2}-\Big(-x\sqrt{4-x^2}+\int \sqrt{4-x^2}\, dx\Big)=\\\\=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}-Q\; \Rightarrow \; \; Q=4\, arcsin\frac{x}{2}+x\sqrt{4-x^2}-Q\; ,](/tpl/images/1075/2260/84be5.png)
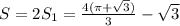

ответ:b3=b1*q^3
b4=b1*q^4
b5=b1*q^5
b6=b1*q^6
Тогда:
b1*q^6-b1*q^4=72
b1*q^3-b1*q^5=9
решаем систему:
b1*q^4(q^2-1)=72
-b1*q^3(q^2-1)=9
Делим первое на второе:
-q=8=>q= -8 - знаменатель прогрессии
b1= -9/(8^3(8^2-1))=-9/(512*63)=1/3584 - первый член прогрессии
Sn=(b1(1-q^n))/(1-q)
S4=(1/3584(1-(-8)^4))/(1+8)=(1/3584*(-4095))/9= -455/3584= -65/512
Объяснение: