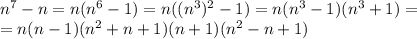. Так как среди любых трех последовательных целых чисел по крайней мере одно делится на 2 и одно на 3, то при любых целых n число 
делится на 
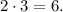Следовательно, число 
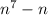делится на 6, если n - любое число. 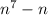делится на 7, если n - натуральное число. Для начала исследуем методом математической индукции
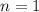имеем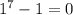 
- кратное 7. 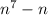делится на 7 при каком-нибудь произвольном натуральном 
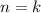, т.е. 
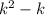кратно 7. 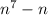делится на 7 и при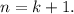 
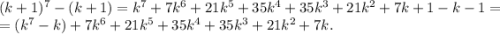
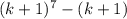картно 7, если n - натуральное число.
D=16+4*32=144
sqrt(D)=12
x1=(-4-12)/2=-8
x2=(-4+12)/2=4
Сумма корней = -8+4=-4. Удачи!