


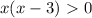
 ∈
∈ 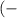 ∞
∞  ∪
∪ 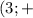 ∞
∞ 

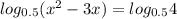
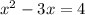
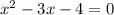
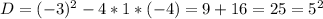
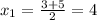
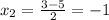



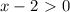
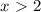
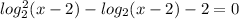

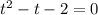

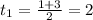

 или
или 
 или
или 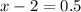
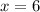 или
или 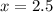

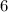
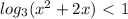

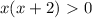
 ∈
∈ 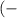 ∞
∞  ∪
∪ 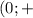 ∞
∞ 




 ∪
∪ 
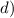
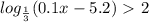







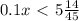



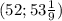
58=29+29
Объяснение:
1) 48+10=58
2) сума двох додатних чисел дорівнює 48+10, запишем 58=a+b, звідси а=х; b=58-х оскільки двох додатних, то х належить проміжку від 0 до 58
3) сума квадратів цих чисел була найменшою, запишем функцією f(x)=a^2+b^2=х^2+(58-x)^2=2x^2-116x+3364
4) знайдемо похідну f(x)
f '(x)=4x-116
5) прирівняємо похідну до нуля
4x-116=0
x=29
6) знайдемо значення функції в критичних точках, тобто на кінцях області визначення (х належить проміжку від 0 до 58) і в точці де похідна дорівнює нулю (х=29), підставив в рівняння f(x)=2x^2-116x+3364 замість х відповідно 0;29;58
f(0)=3346
f(29)=1682
f(58)=3364
7) виберемо найменше значення з отриманих (оскільки нас цікавить, щоб сума була найменшою)
min[0;58] f(x)= f(29)=1682 (тобто при х=29, значення функції буде найменшим і дорівнюватиме 1682)
8) ми знайшли х при якому значення функції буде найменшим (оскільки нас цікавить, щоб сума була найменшою), тепер повернемось до пункта 2 і знайдемо значення а=х і b=58-х для головного рівняння 58=a+b
а=29; b=58-29=29
9) у рівнянні 58=a+b замінемо a i b відповідними значеннями
58=29+29
(на фотографії запис, оформлення даного завдання)

S4=2,5
Sбескон.=8/9
Объяснение:
Сначала найдем первые 4 члена прогрессии (необязательно):
b1= 4/3*1=4/3
b2=4/3*2=4/6=2/3
b3=4/3*3=4/9
b4=4/3*4=4/12=1/3
Их сумма:
q=2/3:4/3=2/3*3/4=1/2
S4=4/3(1-(1/2)^4)/1-1/2=4/3-(1-1/16)/1/2=( 4/3*15/16):1/2=5/4:1/2=2,5
q(p1)=1/2:2=1/4
p1=2/3
S=p1/1-q
S= 2/3/1-1/4=2/3:3/4=8/9