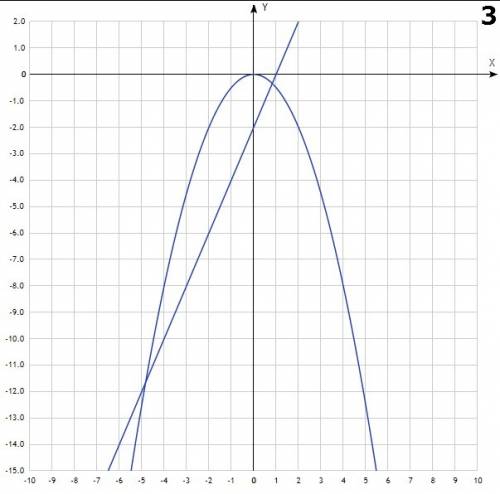
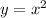- это парабола, с вершиной в точке (0;0). Она симметрична относительно оси OY. Ветви направлены вверх. Проходит через точки (0;0), (2;4), (-2;4)
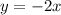- это прямая, для её построения достаточно 2х точек. Например (0;0) и (-2;4)
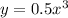- кубическая парабола. График симметричен относительно начала координат, т.е. точки (0;0). 
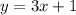- прямая, проходящая через точки (0;1), (1;4)
- прямая, проходящая через точки (0;-2) и (1;0)
- парабола, с вершиной в точке (0;0), симметричная относительно OY. Ветви направлены вниз. 
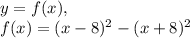
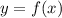— прямая пропорциональность.
— прямая пропорциональность, то есть доказать, что в выражении 
находится в первой степени 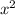(не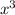 
, не 
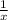, не 
и не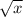 
, а просто ).. Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид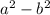 
, где 
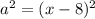, и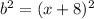 
. Формула «разность квадратов» раскрывается так: 
.
.
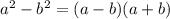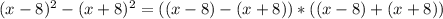
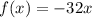, находится в первой степени, а значит зависимость — есть прямая пропорциональность. Доказано.
Объяснение:
Графіком функції y=x^2 є парабола, вітки якої напрямлені вгору. тому щоб побудувати графік, нам достатньо 4-ох точок. Вже при побудові видно, що при значені фінкції у=4, х=2 або х=-2.