Объяснение:
Сначала выведем формулу У(х)
(4x - 4)*y = - 4*x
y = - 4*x/(4*(x-1) = - x/(x-1) - функция для анализа.
1. Область определения функции - ООФ.
Не допускается деление на 0 в знаменателе.
x -1 ≠ 0. x≠ 1
D(y) = R\{1} = (-∞;1)∪(1;+∞) - ООФ.
2. Вертикальная асимптота - x = 1 - разрыв II-го рода.
3. Пересечение с осями координат.
С осью ОХ: числитель равен 0. X0 = 0 - нуль функции.
С осью ОУ: y(0) = 0.
4. Интервалы знакопостоянства.
Положительна: y(x)>0: X∈(0;1).
Отрицательна: y(x)≥0: X∈(-∞;0]∪(1;+∞).
5. Проверка на чётность.
y(-x) = х/(-x-1) - функция общего вида.
6. Первая производная - поиск экстремумов.
y'(x) = -x/(x-1)² -1/(x-1) = 1/(x-1)² = 0
Корней нет. Разрыв при Х = 1.
7. Локальные экстремумы в точке разрыва..
минимум:Ymin = lim{x-> 1-} . Ymin= -∞.
максимум:Ymax = \lim{x-> 1+} y(x) = +∞
8. Интервалы монотонности.
Производная положительная - функция возрастает во всем интервале существования..
Возрастает: X∈(-∞;1)∪[1;+∞).
9. Вторая производная - поиск точек перегиба.
y"(x) = - 2/(x-1)³ = 0
Корней нет.
10. Поведение функции.
Выпуклая - "горка" - X∈(1;+∞).
Вогнутая - "ложка" - X∈(-∞;1)
11. Наклонная асимптота: y = k*x+b.
k = lim(+∞) Y(x)/x = lim (-1/(x-1) = 0 - наклона нет.
b = lim(+∞)Y(x) - 0*x = -x/(x-1) = -1 - сдвиг по оси ОУ.
Горизонтальная асимптота: y = -1.
12. Рисунок с графиками исследования - в приложении.
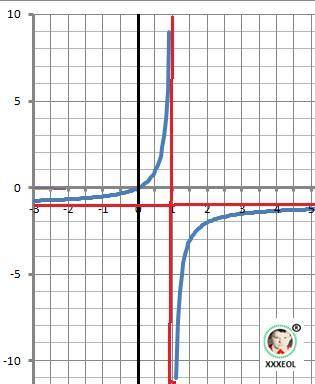
Каждой точке (х; у) графика у = f(x) соответствует единственная точка (х; - у) графика у =- f(x) и наоборот. Точки (х; у) и (х; - у) симметричны относительно оси ОХ. Значит, графики у =f(x) и y = -f(x) симметричны относительно оси ОХ.
Пример 1
Построить график функции у = - .
Решение
Строим график функции у = , а затем строим симметрично относительно оси ОХ.
Симметрия относительно оси ОУ (оси ординат)
Каждой точке (х; у) графика у = f(x) соответствует единственная точка (-х; у) графика у = f(-x), и наоборот. Но точки (х; у) и (-х; у) симметричны относительно оси ОУ, значит, графики у = f(x) и у = f(-x) симметричны относительно оси ОУ.
Пример 2
Построить график функции у = .
Решение
Строим график функции у =, а затем строим симметрично относительно оси ОУ.
Пример 3
Построить график функции у = -
Решение
Выполним ряд последовательных преобразований:
строим график функции у = ;
строим симметрично относительно оси ОУ, т. е. получаем график функции у = ;
строим симметрично относительно оси ОХ, т.е. получаем искомый график функции у = -.
Параллельный перенос (сдвиг) вдоль оси абсцисс
Пусть дан график функции у = f(x).
Чтобы построить график функции у = f(x+a), где а – некоторое данное число, достаточно график функции у= f(x) перенести параллельно направлении оси ОХ на расстояние в положительном направлении, если а<0, и в отрицательном направлении, если а>0.
Пример 4.
Построить графики функций у =(х - 3)² и у =(х + 1)².
Решение
Строим график функции у = х² (пунктиром). Переносим его дважды: в положительном направлении оси ОХ на расстояние, равное 3, и получаем график у = (х – 3)²; в отрицательном направлении оси ОХ на расстояние, равное 1, и получаем график у = (х + 1)².
Параллельный перенос (сдвиг) вдоль оси ординат
Пусть дан график функции у =f(x).
Чтобы построить график функции у = f(x) + a, где а – некоторое данное число, достаточно график функции у = f(x) перенести параллельно оси ОУ на расстояние в положительном направлении, если а >0, и в отрицательном, если а /I>0.
Пример 5.
Построить график функции у = 5+.
Решение
Строим график у = (пунктиром). Переносим его в положительном направлении оси ОХ на расстояние, равное 4, и получаем график у =, а затем переносим в положительном направлении оси ОУ на расстояние, равное 5, получаем искомый график у = 5 +.