Дугу можно измерять угловой мерой (размер центрального угла, опирающего на дугу) или длиной (угловая мера умноженная на радиус). Числовая окружность имеет радиус 1, поэтому значение угловой меры численно равно значению длины.
Половина окружности это π и это же длина дуги (для числовой окружности).
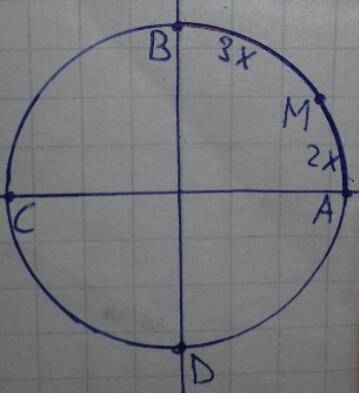
∪AC = π = 2·∪AB ⇒ ∪AB = 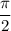
Пусть ∪AM =  , тогда ∪MB =
, тогда ∪MB = 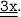
Т.к. первая четверть это ∪AB.
∪AM + ∪MB = 2x+3x = 5x = 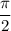 ⇒
⇒
x = 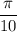 ⇒
⇒ 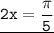 ;
; 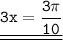
∪DM = ∪DA + ∪AM = 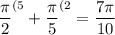
∪MC = ∪MB + ∪BC = 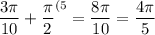
ответ: длина ∪AM = 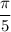
длина ∪MB = 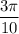
длина ∪DM = 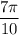
длина ∪MC = 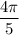
ответ: 50 м и 60 м
Объяснение: Пусть длина участка x м, а ширина - y м, тогда площадь участка равна xy, а периметр равен 2·(x + y).
Составим систему уравнений:
xy = 3000
2x + 2y = 220
Второе уравнение разделим на 2:
xy = 3000
x + y = 110
Решим систему подстановки:
xy = 3000
x = 110 - y
(110 - y)·y = 3000
110y - y² = 3000
-y² + 110y - 3000 = 0
y² - 110y + 3000 =0
D = b² - 4ac = (-110)² - 4·3000 = 12100 - 12000 = 100
x₁ = 110 + √100 / 2 = 110 +10 / 2 = 60
x₂ = 110 - 10 / 2 = 50
y₁ = 110 - 60 = 50
y₂ = 110 - 50 = 60
Решением системы являются две пары чисел (60; 50) и (50; 60). Следовательно, стороны прямоугольника равны 50м и 60м.