ответ: 60 см
Объяснение:
Пусть гипотенуза прямоугольного треугольника х см, ( х>16) тогда согласно условия задачи, один из катетов равен (х-16) см, а другой катет равен (х-2) см.
По Теореме Пифагора следует:
х²=(х-16)²+(х-2)²
х²=х²-32х+256+х²-4х+4
х²-х²+32х-256-х²+4х-4=0
-х²+36х-260=0 (* на (-1)
х²-36х+260=0
х1,2=(36+-D)/2
D=√(36²-4*1*260)=√(1296-1040)=√256=16
х1,2=(36±16)/2
х1=(36+16)/2
х1=26
х2=(36-16)/2=10 - не подходит, так как х>16
Тогда катеты равны 26-16=10 26-2=24
Периметр это есть сумма всех трех сторон:
Р=26+10+24=60 см
ответ : 60 см
через данную точку, мы должны, взять значение икса в данной точке, и подставить данное значение в функцию:
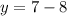
Объяснение:
4x²-7x+a=0
x1+x2=-(-7/4)=7/4
x1+x2+3x2=1
7/4+3x2=1
3x2=-3/4
x2=-1/4
x1+4×(-1/4)=1
x1-1=1
x2=1
x1×x2=c/a=c/4
В данном случае c=a(параметру)
x1×x2=a/4
a/4=2×(-1/4)
a/4=-1/2
a=-2
ответ:-2