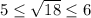
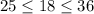
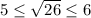Задание 3 N21.6 Доказать что кратно 7

Question

Алгебра: Задание 3 N21.6 Доказать что кратно 7

makc0001 · Accepted Answer

Задание. Какие из чисел √18,√26,√30 заключены между числами 5 и 6.
Решение:
Проверим, заключен ли между числами 5 и 6 число √18, т.е., оценивая в виде двойного неравенства, получим
$5 \leq \sqrt{18} \leq 6$
Возведем все части неравенства в квадрат, будем иметь
$25 \leq 18 \leq 36$
Отсюда следует, что число √18 не заключен между числами 5 и 6, т.к. неравенство 25<18 не верное.

Проверим теперь для √26, т.е. $5 \leq \sqrt{26} \leq 6$ . Возведя все части неравенства в квадрат, получим 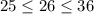$25 \leq 26 \leq 36$ . Неравенства выполняются, следовательно, число √26 заключен между числа 5 и 6.

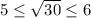Проверим теперь для √30, то есть, $5 \leq \sqrt{30} \leq 6$ . Возведя все части неравенства в квадрат, получим: 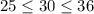$25 \leq 30 \leq 36$ . Видим, что неравенства правильны, следовательно, число √30 заключен между числа 5 и 6.

ответ: √26 и √30.

MOGZ ответил