log(4) (x + 2) - log(4) (x + 5) < 1
log(a) b a>0 b>0 a≠1
log(a) b - log(a) c = log(a) b/c
x+2>0 x>-2
x+5>0 x>-5
ОДЗ x∈(-2 +∞)
log(4) (x + 2) - log(4) (x + 5) < 1
log(4) (x + 2) / (x + 5) < log(4) 4
основание больше 1 снимаем логарифмы без изменения знака
(x + 2) / (x + 5) < 4
(x + 2)/(x + 5) - 4 < 0
(x + 2 - 4x - 20)/(x + 5) < 0
(- 3x - 18)/(x + 5) < 0
- 3(x + 6)/(x + 5) < 0
(x+6)/(x+5) > 0
-------------- (-6) ++++++++++ (-5) -------------------
x∈(-∞ -6) U (-5 +∞)
пересекаем с ОДЗ
x∈(-2 +∞)
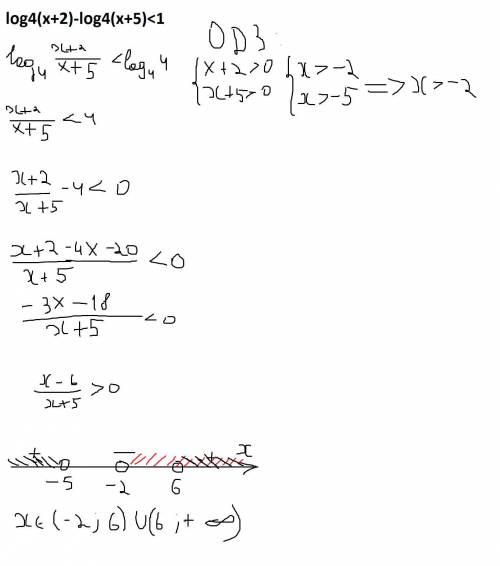
Находим точки, в которых неравенство равно нулю:
x-1=0 x=1
x+5=0 x=-5
Наносим на прямую (-∞;+∞) эти точки:
-∞-51+∞
Получаем три диапазона: (-∞;-5) (-5;1) (1;+∞)
Для того, чтобы определить знак диапазона достаточно подставить хотя бы одно число из этого диапазона:
(-∞;-5) Например, подставим число -7: (-7-1)(-7+5)=-8*(-2)=16>0 ⇒ +
(-5;1) Подставим число этого диапазона 0: (0-1)(0+5)=-1*5=-5<0 ⇒ -
(1;+∞) Подставим 2: (2-1)(2+5)=1*7=7>0 ⇒ +
-∞+-5-1++∞ ⇒
x∈(-∞;-5)U(1;+∞).