Объяснение:
a) По условию составляем неравенство
-2x^2 + 2x -3 > -x -1
-2x^2 + 3x -2 > 0
2x^2 - 3x + 2 < 0
x^2 - 1.5x + 1 < 0
(x^2 - 0.75)^2 + 1 < 0 - не может быть ни при каких x, потому что значение выражения (x^2 - 0.75)^2 + 1 всегда положительно, значит, f(x) не будет больше g(x) ни при каких значениях x.
б) График функции y = f(x) находится ниже графика функции y =g(x), значит, выполняется неравенство f(x) < g(x)
x/3 < 6/x
x/3 - 6/x < 0
(x^2 - 18)/3x < 0
1. 
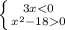3x < 0 ⇒ x<0 ⇒ x < -
(x + )(x - ) > 0 ⇒ x < - или x>
2. 
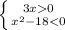3x > 0 ⇒ x>0
(x + )(x - ) < 0 ⇒ x < и x>- ⇒ 0<x <
x < - и 0<x <
Очень найдите ( sin5α + sinα , если sinα = 1/√5
"решение" : * * * sinα +sinβ =2sin( (α+β)/2 ) *cos( (α - β)/2 ) * * *
sin5α + sinα = 2*sin ( (5α +α)/2 ) *cos ( (5α -α)/2 ) =
2*sin3α*cos2α =2*(3sinα - 4sin³α)* (1 -2sin²α ) = || sinα = 1/√5 || =
=2*(3 /√5 - 4 / 5√5)* (1 - 2* 1/5 ) = 2*( ( 3*5 - 4) / 5√5 )*( (5*1 -2)5 ) =
=2* (11 / 5√5) * (3/5) = 66/25√5 = 66√5 / 125
ответ: 66√5 / 125
* * * P.S. sin3α =sin(2α+α) = sin2α*cosα+ cos2α*sinα =
2sinα*cosα*cosα + (cos²α -sin²α)*sinα =sinα *(2cos²α + cos²α - sin²α) =
sinα *(3cos²α - sin²α) = sinα *( 3(1 -sin²α) - sin²α ) = 3sinα - 4sin³α * * *