Объяснение:
Как я понял, задача состоит в нахождении наибольшего значения функции. Для это необходимо найти производную этой функции и приравнять ее к 0 .
Правила взятия производной, необходимые для решения этого примера:
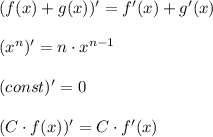
Эти правила можно описать следующим образом :
· Производная от суммы функций равна сумме их производных.
· Производная степенной функции равна произведению показателя степени на функцию, с показателем степени на 1 меньше исходного.
· Производная от постоянной величины равна 0.
· Постоянный множитель можно вынести за знак производной.
Тогда производная заданной функции равна :
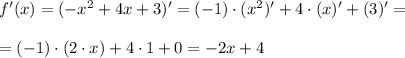
Приравняем производную к 0 и найдем корень уравнения:
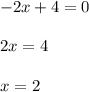
Подставим найденное значение в исходную функцию:
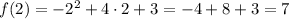
Получили, что наибольшее значение функции равно 7 в точке x=2
№1
((3x-4/x+1 - 2x-5/x+1 + x/x+1 )/(x/x^2-1)) =
Делю пополам уравнения и по действиям, думаю, что вы поймете.
Начну с конца.
(x/x^2-1) = ((x+1)(x-1)/x) \\ Умножим числитель на величину, обратную знаменателю x/x^2-1
((3x-4-(2x-5))/x+1) + x/x+1)) = (1+x/x+1) \\ Поделили на две части уравнения, и пришло время - Объединить пример.
(1+x/x+1) * ((x+1)(x-1))/x) \\ В данном уравнении, первую дробь Умножаем на знаменатель и получаем вывод:
(1(x+1)/1(x+1) + x/x+1)
((2x+1)(x+1) * ((x+1)(x-1)/x) =((2x+1)/1)((x-1)/x) =(2x+1)(x-1)/x
ответ на первый пример: (2x+1)(x-1)/x
№2
Не особо понял мысль твоего уравнения, в следующий раз, будьте добры, отправлять фотографию примера, иногда бывает, что за готовое решение ставят жалобу и человек, который решал дают страйк!
(a - a^2-3/a-2): 3-2a/4-4a+a^2 =
Так же как и в первом случае, начну с конца!
Переворачиваем дробь :
((4-4a+a^2)/3-2a) = ((2-a)^2)/(3-2a) \\ Получили по формуле квадратного уравнения!
Вернемся к первой части, домножаем уравнение на (a-2)
(a(a-2)/(a-2) - (a^2-3)/(a-2)) * (((2-a)^2)/(3-2a));
=>Скомбинируем уравнение и получаем:
((-2a+3/a-2))/((2-a)^2/(3-2a)) =
Упростим числитель и его члены
=> )(2-a)^2/(a-2) =>
(a-2)(a-2)/(a-2)*1 = > a-2
ответ: a-2