Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот
Объяснение:
Выясним, при каких значениях переменной функция 3 x + 1 x − 2 не определена. x = 2
Рассмотрим рациональную функцию
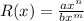, где n - степень числителя, а m - степень знаменателя.
1. Если n < m , то ось x, y = 0 , является горизонтальной асимптотой.
2. Если n = m , то горизонтальной асимптотой является прямая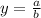 
Если n > m , то не существует горизонтальной асимптоты (только наклонная асимптота).
Найдем n и m
n = 1 ; m = 1
Поскольку n = m , горизонтальная асимптота является прямой 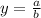, где a = 3 и b = 1
y = 3
Наклонных асимптот нет, поскольку степень числителя меньше либо равна степени знаменателя.
Это множество всех асимптот.
Вертикальные асимптоты: x = 2
Горизонтальные асимптоты: y = 3
Нет наклонных асимптот
это не пример, а система уравнений)
х-4у=10
(х-1)²=7(х+у)+1
упростим второе уравнение.
в левой части дана формула сокращенного умножения, разложим ее. чтобы раскрыть скобки из правой части, нужно член, стоящий перед скобкой, умножить на каждый член в скобках. получим:
х-4у=10
х²-2х+1=7х+7у+1
во втором уравнении перенесем все в левую часть, поменяв знак, если переносим выражение через равно. приведем подобные и получим:
х-4у=10
х²-9х-7у=0
решим систему методом подстановки.
выразим х в первом уравнении:
х=10+4у
х²-9х-7у=0
теперь вместо х подставляешь выражение 10+4у во второе уравнение.
х=10+4у
(10+4у)²-9(10+4у)-7у=0
поработаем со 2 уравнением. раскроем скобки:
100+80у²+16у-90-36у-7у=0
80у²-27у+10=0
D= 729-3 200
дискриминант выходит отрицательный, значит корней нет
я так думаю...
Объяснение: