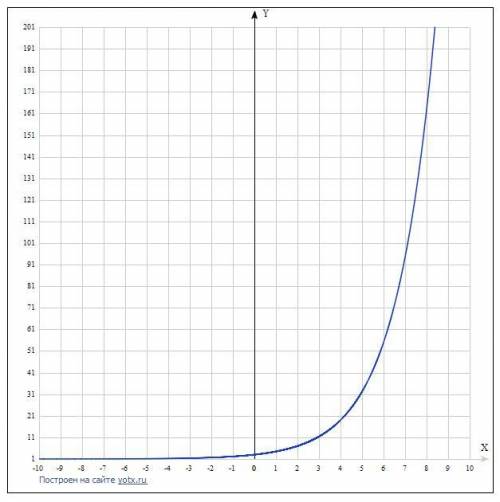
![\int e^7(7-e^{-4x})7x^2\, dx=\int 49e^7\cdot x^2\, dx-7e^7\int x^2e^{-4x}\, dx=\\\\=[u=x^2\; ,\; du=2x\, dx\; ,v=-\frac{1}{4}e^{-4x}\; ]=\\\\=49e^7\cdot \frac{x^3}{3}-7e^7\cdot \Big (-\frac{1}{4}\, x^2e^{-4x}+\frac{1}{2}\int x\, e^{-4x}\, dx\Big )=\\\\=\frac{49e^7}{3}\, x^3-7e^7\cdot \Big (-\frac{1}{4}\, x^2\, e^{-4x}+\frac{1}{2}\cdot (-\frac{1}{4}x\, e^{-4x}+\frac{1}{4}\int e^{-4x}\, dx)\Big )=\\\\=\frac{49e^7}{3}\, x^3-7e^7\cdot \Big (-\frac{1}{4}\, x^2\, e^{-4x}-\frac{1}{8}\cdot x\, e^{-4x}-\frac{1}{32}\, e^{-4x}\Big )](/tpl/images/1044/2829/2fd21.png)
 часов. Но они разгружали х+12 ящиков, справившись с работой за
часов. Но они разгружали х+12 ящиков, справившись с работой за 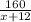 часов, что на 3 часа раньше срока.
часов, что на 3 часа раньше срока. -
- 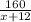 = 3
= 3 -
- 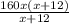 = 3х(х+12)
= 3х(х+12) =
= 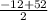 = 20
= 20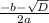 =
= 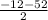 = -32 - не подходит, т.к. х<0
= -32 - не подходит, т.к. х<02) D(y)=(-∞; -6]∪[1; +∞)
3)Смотреть изображение
4)-9; 3
Объяснение:
2) Область определения ф-ции - все значения, которые может принимать независимая переменная (х). Подкоренное выражение корня чётной степени должно быть не меньше нуля, поэтому чтобы найти область определения нужно решить неравенство
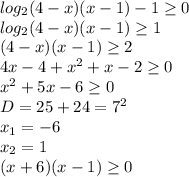
x∈(-∞; -6]∪[1; +∞)
Тогда D(y)=(-∞; -6]∪[1; +∞)
3) Чтобы построить график функции нужно построить график обычной показательной функции без второстепенных коэффициентов. Берём любые значения икса и считаем чему при данных значениях будет равен игрек. Точки с полученными координатами выставляем на координатную плоскость и проводим через эти точки график функции. Потом смещаем график в соответствии с коэффициентами. Свободные коэффициенты указывают на сколько клеток нужно сместить график по ординате. Коэффициент перед иксом Сжимает график по абсциссе обратить внимание, что данная функция является показательной и абсцисса здесь будет являться асимптотой, и график её никогда не пересечёт, хотя будет всё больше и больше приближаться к ней.
4)
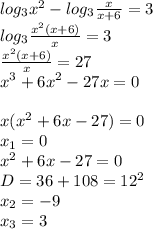
Не забываем про ОДЗ
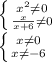
С учётом ОДЗ корень 0 не является корнем уравнения. В ответ идут только -9 и 3