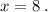Решение: Обозначим первоначальную массу олова в сплаве за (х) кг, тогда процентное содержание олова в сплаве составляет: х/16*100% При добавлении олова, масса сплава стала равной: 16+2=18(кг) а содержание олова в новом сплаве составило: (х+2) кг процентное содержание олова в новом сплаве равно: (х+2)/18*100% А так как в новом сплаве содержание олова на 5% больше чем в первоначальном сплаве, составим уравнение: (х+2)/18*100% - х/16*100%=5% 100*(х+2)/18 - 100*х/16=5 Приведём к общему знаменателю 144 8*100*(х+2) - 9*100*х=144*5 800х+1600 -900х=720 -100х=720-1600 -100х=-880 х=-880 : -100 х=8,8 (кг) -первоначальное количество олова в сплаве
ответ: Первоначальное количество олова в сплаве 8,8кг
ответ: 1-Б , 2 - Г , 3 - E , 4 - A .
Объяснение:
ответ: Б)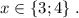
ответ: Г)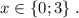
ответ: Е)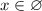 .
.
ответ: А)