ответ: приложено
Объяснение:
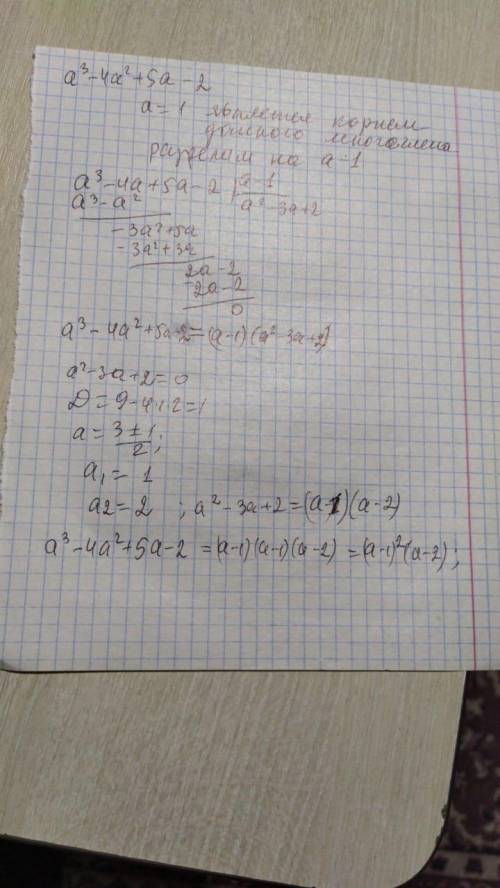
 , где A, B, C - координаты нормального вектора плоскости N(A,B,C).
, где A, B, C - координаты нормального вектора плоскости N(A,B,C). ⇒ N(2,-3,4).
⇒ N(2,-3,4). , где
, где 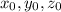 - координаты точки M(
- координаты точки M(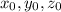 ), через которую проходит прямая,
), через которую проходит прямая,  - координаты направляющего вектора S(
- координаты направляющего вектора S( ).
). ) = N(A,B,C) ⇒ N(2,-3,4) = S(2,-3,4); M(1,-2,3).
) = N(A,B,C) ⇒ N(2,-3,4) = S(2,-3,4); M(1,-2,3).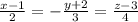
Алгоритм:
Как разложить уравнение высшей степени. По теореме Безу найти корень уравнения. Если найти корень не получается попробовать 1/2 и -1/2. Иначе подбирать (рекомендую ±1/3, ±2/3 и т.п.)
По схеме Горнера или уголком поделить уравнение на (x-a), где a - найденный в пункте 1 корень.
Продолжать до тех пор, пока в качестве одного из множителей не получится квадратное уравнение.
Применить алгоритм разложения на множители квадратного уравнения.
(как делать это быстро: подобрать корень, и подогнать под (x-a))