Решим задачу пошагово:
cos(х-π/3)+cos²2x=1-cos²(π/2-2х)
cos(х-π/3)+cos²2x - 1 = -cos²(π/2-2х)
cos²(π/2-2х) =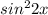 
(По формуле приведения).
cos(х-π/3)+cos²2x - 1 = -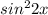
cos²2x - 1 = (cos2x - 1)(cos2x + 1).
(cos2x - 1) = 1 - 2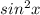
- 1 = - 2.
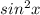(cos2x + 1) = 2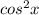
- 1 + 1 = 2.
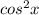(cos2x - 1)(cos2x + 1) = -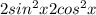 
= -
=-
= -.
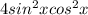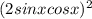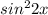После подстановки найденных тождеств, получим:
cos(х-π/3) - = -.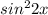
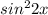cos(х-π/3) - 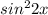+ 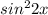= 0.
cos(х-π/3) = 0.
cos(х-π/3) = cos(π/2 + πn), где n принадлежит Z.
х-π/3 = π/2 + πn, где n принадлежит Z.
x = π/2 + πn + π/3, где n принадлежит Z.
x = 5π/6 + πn, где n принадлежит Z.
Найдём корни, принадлежащие отрезку [-π;2π], для этого составим следующее двойное неравенство:
-π >= 5π/6 + πn <= 2π, знаки >= и <= - это соответственно больше или равно и меньше или равно.
-π - 5π/6 >= πn <= 2π - 5π/6
- 11π/6 >= πn <= 7π/6
- 11/6 >= n <= 7/6
- 1 >= n <= 1.
Теперь находим корни.
При n = -1, x = - 4π/6.
При n = 1, x = 11π/6.
При n = 0, x = 5π/6.
Найдём их среднее арифметическое:
(- 4π/6 + 11π/6 + 5π/6)/3 = 2π/3.
ответ: 2π/3
Как известно, если есть две периодические функции с периодами T1 и T2 , то периодом их суммы, разности и частного является число T, кратное T1 и T2.
Период sinx = 2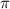
k, где k - целое число.
Период tgx = 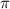n, где n - целое число.
Наименьшим положительным периодом будет являться число 2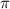, так как при k = 1 и n = 1, оно кратно обоим периодам.
Теперь проверим, что 2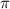 действительно является периодом функции:
f(x) = f( x + T), f( x + 2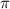) = sin(x + 2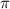) + tg(x + 2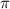) = sinx + tgx.
Как видно из вышенаписанного, число 2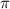 действительно является периодом функции y=sinx+tgx и является её наименьшим положительным периодом.
ответ: 2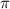
f(x)=-x²-2x+a
Це парабола з вітками донизу, найбільше значення на вершині. Рахуємо координати вершини.
хв=(2/-2)=-1
ув=-1+2+а=а+1
g(x)=|x-a|+6-3a
Найменше значення досягається при х=а:
g(x)=|0|+6-3а=6-3а
Прирівнюємо
а+1=6-3а
4а=5
а=1.25
Відповідь: 1.25
Если будут вопросы – обращайтесь :)