Решим неравенства: (1) x > 35 (2) x ≤ 99 (3) x > 8 (4) x ≥ 10 (5) x > 5
Если верно неравенство (1), то автоматически верны неравенства (3), (4) и (5), и верных неравенств не меньше 4, хотя по условию их только 3. Значит, неравенство (1) неверно, x ≤ 35, откуда следует, что неравенство (2) верно.
Среди оставшихся неравенств (3), (4) и (5) должны быть два верных и одно неверное. Если верно неравенство (4), то сразу же верны и остальные неравенства, чего быть не должно, поэтому неравенство (4) неверно, а неравенства (3) и (5) верны.
Системе неравенств 5 < 8 < x < 10 ≤ 35 ≤ 99 удовлетворяет единственное натуральное число x = 9.
Объяснение:
8.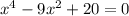
Замена: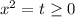
Обратная замена: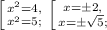
9.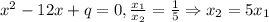
По теореме Виета: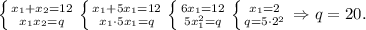
Второй корень: x₂= 5 · 2 = 10.
10.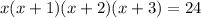
Отдельно перемножим первый и четвертый, второй и третий множители:
Замена: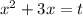
Обратная замена:
Итого: x₁ =-4, x₂ = 1.