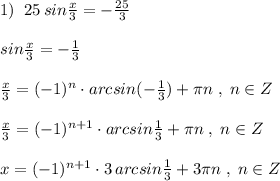
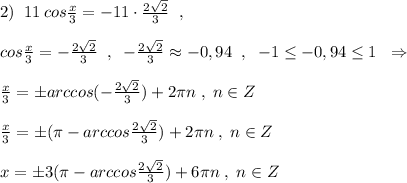
1) эти графики параллельные прямые смещенные относительно друг друга на 4 еденицы по оси y
2) эти графики перпендекулярны друг другу и пересекаются в точке
-5x-1=5x-3, т .е. в точке x=1/5 y=-2
3) пересекаются под некоторым острым углом в точке 2x+1=3x+1, т.е. в точке x=0 y=1
все вышеуказанное основанно не на сложных рассчетах, а на сравнении коэффицентов стоящих при x. Эти коэффиценты называются угловыми коэффицентами и являются tg угла между прямой и осью ox.
уравнение прямой с угловыми коэффицентами выглядит как y=kx+b, где k-кгловой коэффицент