y = f(x)
Сначала осознаем как должен выглядеть график (рис. 1):
Рисуем прямые x = -5 и x = 6, график не должен выходить за эти прямые (обозначили область определения).Рисуем прямые y = -4 и y = 3, график не должен выходить за эти прямые (обозначили множество значений).На оси Ox отмечаем интервал (1;4), график функции должен проходить через ось Ox в этом интервале (обозначили промежуток нулевого значения).Теперь построим график функции (рис. 2):
Для простоты построим график ломанной (она непрерывна и просто изображается).
Функция убывает на всей области определения, поэтому для самого меньшего х из области определения , должно быть самое наибольшее y из множества значений (потом это значение уже не реализуется т.к. функция убывает, тогда множество значений будет другим). Итог: вершина ломанной в точке (-5;3).Пусть следующая вершина в точке (0;2).Ноль функции, он же пусть будет и вершиной ломанной, в точке (3;0) т.к. 3 ∈ (1;4).Последняя вершина в точке (6;-4), y= -4 для нужного множества значений.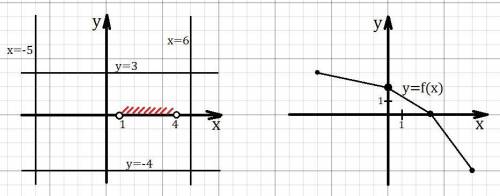
Объяснение:
составим систему уравнений
b(5)-b(3)=1200 (1)
b(5)-b(4)=1000 (2) ⇒ b(5)= 1000+b(4) (2_2)
Добавим в систему третье уравнение b(4)²=b(5)*b(3) (3)
вычтем из уравнения (1)-(2) ⇒ b(4)-b(3)=200 ⇒ b(3)=b(4)-200 (4)
Подставим (2_2) в (3)
b(4)²=(1000+b(4))*b(3) Подставим вместо b(3) уравнение (4)
b(4)²=(1000+b(4))*(b(4)-200)
b(4)²==1000b(4)+b(4)²-200000-200b(4) [b(4)² сократим]
800 b(4)=200000 b(4)=250
b(3)=250-200=50 b(3)=50
q=b(4)/b(3)=250/50=5 q=5
b(3)=b(1)*q² ⇒ b(1)=50/25=2 b(1)=2
S(5)= b(1)(q^n-1)/(q-1)
S(5)=3125
ответ см. в приложении